20. Para o circuito da figura 10.83:
a) Determine a constante de tempo do circuito.
b) Escreva a equação matemática para a tensão depois que a chave é fechada.
c) escreva as equações para corrente e a tensão .
d) Faça um esboço das formas de onda de e .
Figura 10.83
Passo 1
Olá galerinha! Vamos de mais um probleminha de circuitos elétricos.
Neste, logo de cara percebemos a diferença de estrutura, porém, muito calma nesta hora, vamos resolver rapidinho.
O que difere mais, é o fato de o circuito ser estar aberto, mas temos a diferença de potencial registrada na imagem, então não há com que se preocupar.
Vamos anotar as informações do problema e tudo ficará claro:
Viu?!, temos C, temos R e temos E, assim como nos outros casos. Então só precisamos seguir nossa receita 😉
Passo 2
a) Vamos calcular a constante de tempo através da relação:
Passo 3
b) Agora vamos encontrar a expressão matemática para a tensão para a constante de tempo de terminada no item anterior. A expressão geral para é dada por:
Agora, basta inserir as informações que temos sobre o problema, assim chegamos à:
Passo 4
c) Escrever a equação para a corrente . De forma análoga ao que foi feito para a tensão , vamos inserir as informações que temos na equação geral da corrente, que é representada por:
Desta forma, obtemos:
Passo 5
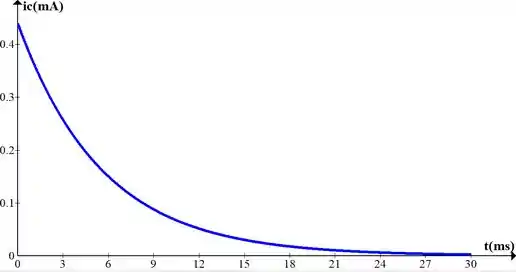
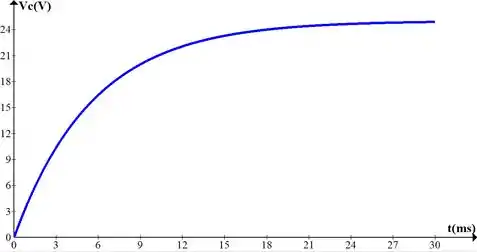
Resposta
a)
b)
c)