Para o circuito da figura 10.81:
a) Determine a constante de tempo do circuito.
b) Escreva a equação matemática para a tensão depois que a chave é fechada.
c) Determine a tensão depois de transcorrida uma, três e cinco constantes de tempo.
d) Escreva as equações para corrente e a tensão .
e) Faça um esboço das formas de onda de e .
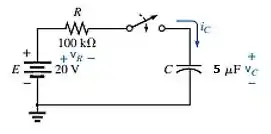
Figura 10.81
Passo 1
 Oi pessoal! Vamos iniciar uma seção um tanto intensa, mas não se preocupe, vamos dar passo pequenos e resolver tudo, então:
Oi pessoal! Vamos iniciar uma seção um tanto intensa, mas não se preocupe, vamos dar passo pequenos e resolver tudo, então:
Como primeiro passo, vamos anotar as informações do problema:
Sempre façam as conversões de unidade nesta etapa, isso evita erros na hora da conta.
Passo 2
Todas as equações que vamos utilizar estão destacadas na seção correspondente, caso se esqueça de alguma, corra lá 🏃♂️ e dê uma conferida!
a) Vamos calcular a constante de tempo através da relação:
Podemos inserir os valores fornecidos pelo problema, e assim obtermos:
![]()
Tenha cuidado com as operações do número com potência de 10, na dúvida, confira!
Passo 3
b) Agora vamos encontrar a expressão matemática para a tensão para a constante de tempo de terminada no item anterior. A expressão geral para é dada por:
Assim, basta inserir as informações que temos sobre o problema, assim chegamos à:
Viu?! Não foi tão difícil assim 😎
Passo 4
c) Agora vamos determinar a tensão para os tempos .
Para poupar um pouco do trabalho, vamos analisar o expoente da função exponencial:
Como os instantes de tempo que vamos analisar são múltiplos de , não há necessidade de calcular t, pois a razão vai ser o fator de multiplicação.

Isso mesmo, não precisamos calcular t! Confira abaixo:
Dessa forma, o expoente, para cada instante, será o valor inteiro obtido acima. Sendo assim, basta inserirmos na equação de encontrada no item anterior.
Passo 5
d) Nesse passo, vamos escrever a equação para a corrente . De forma análoga ao que foi feito para a tensão , vamos inserir as informações que temos na equação geral da corrente, expressa por:
Desta forma, obtemos:
Perceba que o foi comprimido no prefixo m da unidade A, que quer dizer mili. Confira as ordens de grandeza nos capítulos iniciais do livro!
Passo 6
Ainda no mesmo item, o livro pede que a expressão matemática para , então vamos novamente, inserir as informações na equação correspondente, e obtermos:
Até esse momento, só precisamos inserir as informações que o problema pede, nas equações já determinadas pelo livro.
Passo 7
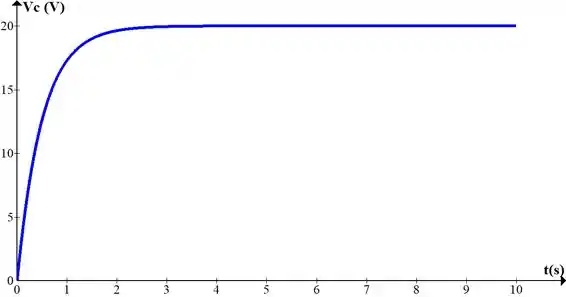
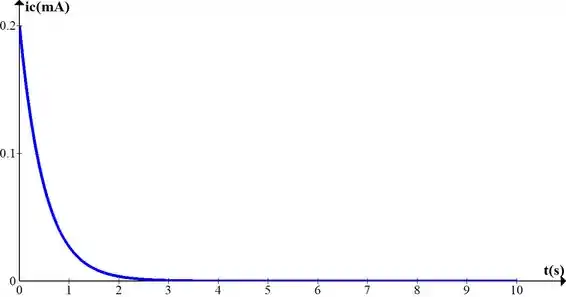
Resposta
a)
b)
c) ; ;
d) ;