Para o circuito da figura 12.70:
a) Determine
b) Escreva uma equação matemática para a corrente após a chave ser fechada em
c) Escreva equações matemáticas para a corrente e após a chave ser fechada em
d) Determine e em e
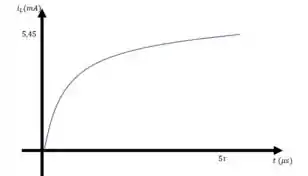
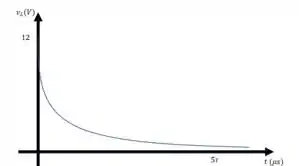
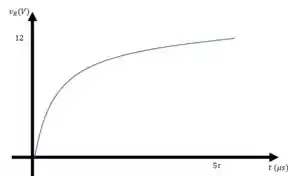
e) Esboce as formas de onda de , e durante a fase de armazenamento
Passo 1
Nesse exercício, vamos trabalhar com esse circuito:
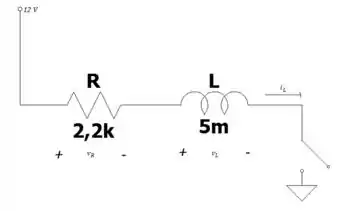
Bora lá analisar esse circuito :D
a) Aqui queremos a constante de tempo do circuito, que no caso do circuito RL é dada por
Substituindo os valores de e :
Então
Passo 2
b) Quando a chave é fechada, a expressão de é dada por
Substituindo os valores:
Fechou?
Passo 3
c) Agora vamos encontrar a expressão de , ela vai ser
Substituindo:
E agora para :
Como :
Certinho??
Passo 4
d) Agora queremos encontrar os valores de e para e :
Temos
Agora para :
Passo 5
Temos
Agora para :
Passo 6
Temos
Agora para :
E é isso pra esse item hahahaha
Passo 7
e) Agora é só a gente esboçar o gráfico de e . A gente precisa lembrar que é a parte final do gráfico, quando sobe completamente ou cai completamente.
Em , para , a corrente vale . Quando , a corrente tende a
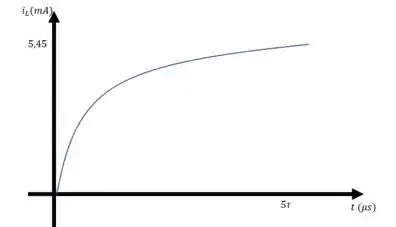
Em , para , a tensão vale . Quando , a tensão tende a 0
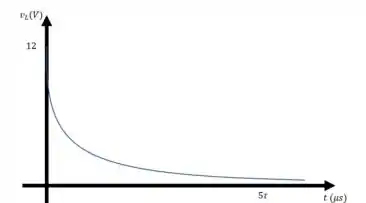
Em , para , a tensão vale . Quando , a tensão tende a
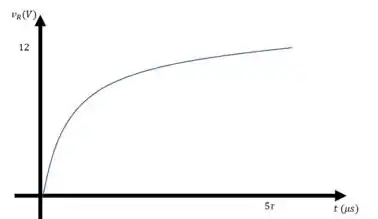
E acabaaaamosss :D
Resposta
a)
b)
c)
d)
e)