23.Para o circuito da figura 10.85
a) Determine a expressão matemática para tensão entre os terminais do capacitor após a chave ter sido colocada na posição 1.
b) Repita o item a para a corrente .
c)Determine a tensão e a corrente se a chave é colocada na posição 2 e decorrer um tempo igual a cinco constantes de tempo do circuito de carga.
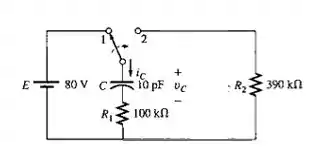
Figura 10.85
Passo 1
E aí galerinha! Vamos resolver mais um probleminha de circuitos elétricos. Daquele mesmo jeitinho, devagar e sempre 😋.
Vamos anotar as informações do problema:
Aproveitem e façam as conversões de unidades nessa etapa. Evitem erros futuro!
Passo 2
a) Calcular a constante de tempo , levaremos em consideração somente o resistor que faz parte da malha fechada, que vamos analisar no primeiro momento:
Passo 3
Ainda no item a – Agora vamos encontrar a expressão matemática para a tensão para a constante de tempo de terminada no item anterior. A expressão geral para é dada por:
Agora, basta inserir as informações que temos sobre o problema, assim chegamos à:
Até aqui, utilizamos o mesmo procedimento dos problemas anteriores 😎
Passo 4
b) Repita o item anterior para a corrente . De forma análoga ao que foi feito para a tensão , vamos inserir as informações que temos na equação geral da corrente, que é representada por:
Desta forma, obtemos:
Pronto! Já fizemos dois itens, estamos quase lá! 😊
Passo 5
c) Agora vamos determinar a tensão para os tempos, para a chave na posição 2.
Para poupar um pouco do trabalho, vamos analisar o expoente da função exponencial:
Como o instante de tempo que vamos analisar é um múltiplo de , não há necessidade de calcular t, pois a razão vai ser o fator de multiplicação, como mostrado abaixo:
Dessa forma, o expoente da exponencial, será o valor inteiro obtido acima. Sendo assim temos:
Passo 6
Ainda no item c - Agora devemos olhar bem para a malha ao qual o problema se refere. Como há dois resistores agora nesta malha, temos que calcular a resistência equivalente.
Escrever a equação para a corrente . De forma análoga ao que foi feito para a tensão , vamos inserir as informações que temos na equação geral da corrente, que é representada por:
Desta forma, obtemos:
Passo 7
d)Trace as formas de onda de e para o intervalo de até
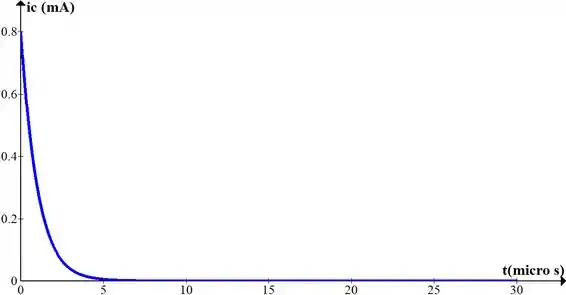
Resposta
a)
b)
c) ;