Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 3.2 - Ex. 1

No circuito da Figura 3.4 troque o resistor de 2Ჲ por um de 1Ჲ, e calcule i, V 1 e a resistência vista pela fonte (isto e, R = 6/i).

Passo 1

Resolvemos esse exercício utilizando o método de análise de malhas da seguinte maneira.

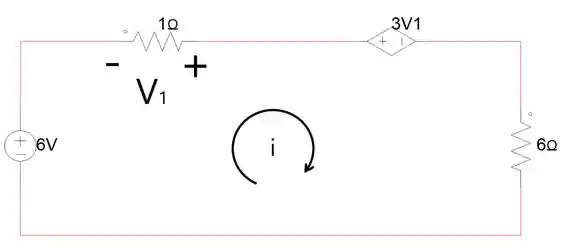
Temos apenas uma malha, portanto teremos uma equação.

Passo 2

Obtemos a equação: - V 1 + 3 V 1 + 6 i = 6 .

Também podemos obter a equação de V 1 : V 1 = - 1 i

Passo 3

Substituindo a equação V 1 na primeira equação, podemos isolar o i .

- - 1 i + 3 - 1 i + 6 i = 6

i - 3 i + 6 i = 6

i = 1,5 A

Sabendo i , podemos agora obter V 1 pela equação: V 1 = - 1 i

V 1 = - 1 ( 1,5 )

V 1 = - 1,5 V

Passo 4

Por fim, para encontrar a resistência vista pela fonte é R = 6 / i .

R = 6 / 1,5

R = 4   O h m

Resposta

i = 1,5 A

V 1 = - 1,5 V

R = 4   O h m

Exercícios de Livros Relacionados

Um circuito é construído a partir de uma fonte de tensão v g , um resistor linear de 2Ω e um resistor não-linear em série. O resistor não linear é representado por v= i 2 Onde v é a tensão sobre o res
Resolva o Prob. 4.29 usando métodos da teoria de gráficos.
Calcule v no Ex. 4.3.1, se o elemento X é uma fonte de tensão dependente de 5i V com o terminal positivo na parte superior.
Usando análise de malhas, encontre i1 e i2 se o elemento x é uma fonte de tensão independente de 6 V, com o terminal positivo na parte superior.
Repita 0 Exerc. 4.5.1 com R1 = 1 Ω , R2 = 2 Ω , R3 = 4 Ω , vg1 = 21 V e vg2 = 0. Verifique os resultados empregando resistência equivalente e divisão de corrente.