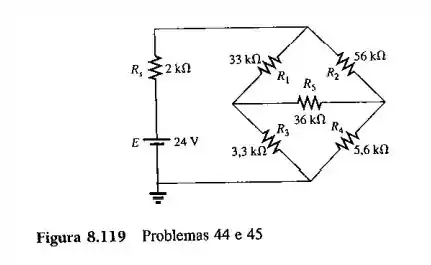
Para o circuito mostrado na Figura 8.119:
- Escreva as equações malha usando a abordagem padronizada.
- Determine a corrente em .
- O circuito está equilibrado?
- A equação (8.4) foi satisfeita?
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
Vamos começar redesenhando a rede da ponte como mostrado na Figura 1

Passo 2
- Vamos considerar o loop 1, na Figura 1, para encontrar a corrente usando a análise de malha.
- Resolvendo a equação (1), equação (2), e equação (3), iremos encontrar os valores atuais correspondentes
- Pela equação (4), a corrente através do , seu valor da resistência é de .
- Consideremos a seguinte expressão para a condição de equilíbrio da ponte.
Vamos considerar o loop 2, na Figura 1, para encontrar a corrente usando a análise de malha.
Vamos considerar o loop 3, na Figura 1, para encontrar a corrente usando a análise de malha.
Assim, a equação (2), equação (3), e equação (4) são as equações de malha para a configuração da ponte.
Onde, as equações de malha são calculadas para a configuração da ponte.
Passo 3
Resolvendo esse sisteminha, temos que:
Portanto, os valores atuais são .
Considere a seguinte fórmula e encontre a corrente através da resistência
Portanto, a corrente através do
Passo 4
Para uma rede balanceada, o valor da tensão ou corrente , deve ser zero.
Portanto, a rede de ponte fornecida está balanceada, pois a corrente através do valor da , resistência é .
Passo 5
Portanto, a rede de pontes dada satisfaz a equação (8.4).
Resposta
- Assim, a equação (2), equação (3), e equação (4) são as equações de malha para a configuração da ponte.
- Portanto, a corrente através do
- Portanto, a rede de ponte fornecida está balanceada, pois a corrente através do valor da , resistência é .
- Portanto, a rede de pontes dada satisfaz a equação (8.4).
Onde, as equações de malha são calculadas para a configuração da ponte