Para o circuito mostrado na Figura 15.129:
a. Determine , e em forma fasorial.
b. Calcule o fator de potência total indicando se é atrasado ou adiantado
c. calcule a potência média fornecida ao circuito
d. Construa o diagrama de impedâncias
e. Construa o diagrama de fasores para as tensões , e e a corrente
f. Calcule as tensões e usando a regra dos divisores de tensão e compare com os resultados do item (a)
g. Desenhe o circuito em série equivalente até o ponto onde se pode relacionar as características do circuito.
Passo 1
Faaaaala galera, tudo bom?
Essas equações ajudarão a gente a calcular
Para , temos:
agora o valor para
Vamos substituir os valores em
Vamos deixar neste formato
o ângulo pode ser obtido dessa forma
e já temos o valor de
Com este valor, vamos calcular o que foi solicitado no item (a)
Substituindo
e para o ângulo
Agora iremos determinar
Não se esqueça que ao contrário de quando determinamos , agora o ângulo será somado
Passo 2
O enunciado pede o fator de potência
Lembra dessa equação?
Só falta substituir os valores
Passo 3
Precisamos da potência média
substituindo
Passo 4
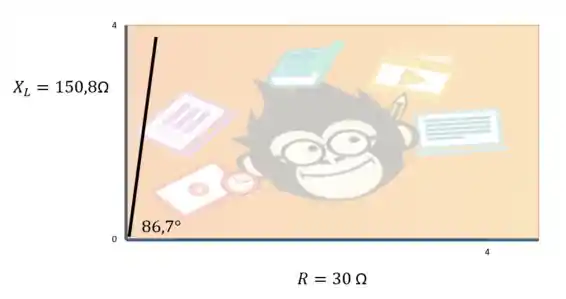
Passo 5
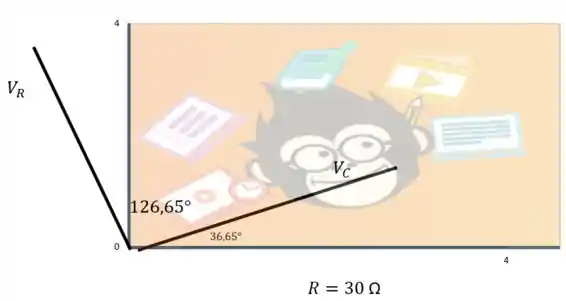
Passo 6
Para esse item, queremos os valores de e . Porém, dessa vez calcularemos eles usando a regra dos divisores de tensão
e para o ângulo
Pronto, de forma semelhante faremos com
concluímos que independente do método vamos chegar aos mesmos resultados
Resposta
a.
b.
c.
d. Resposta no Passo 4
e. Resposta no Passo 5
f.
g.