Para o circuito em paralelo visto na Figura , plote o gráfico:
- De e em função da frequência para a faixa de frequência de a .
- De em função da frequência para a faixa de frequência do item (a).
- De em função da frequência para a faixa de frequência do item (a).
Passo 1
Opa galera, tudo certinho ai? Vamos resolver esta questão.
Temos três itens nos pedindo para plotar diferentes gráficos a partir da figura do enunciado.
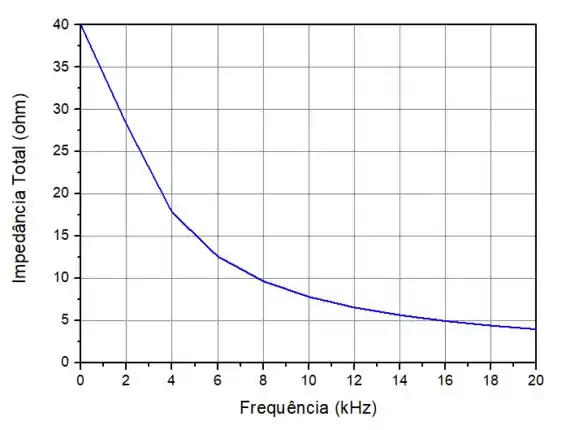
O item (a) quer os gráficos da impedância total e do ângulo de fase total em função da frequência na faixa de a .
Para isto precisamos descobrir os valores de e .
Passo 2
Vamos calcular a impedância do Capacitor:
Substituindo os valores, temos que:
Logo:
E a admitância no capacitor será:
A admitância no resistor vale:
E sabendo que:
Temos que:
Portanto:
O ângulo de fase de admitância vale:
Passo 3
Sabendo que:
Temos que:
E:
Plotanto os gráficos na faixa de frequência solicitada, temos que:
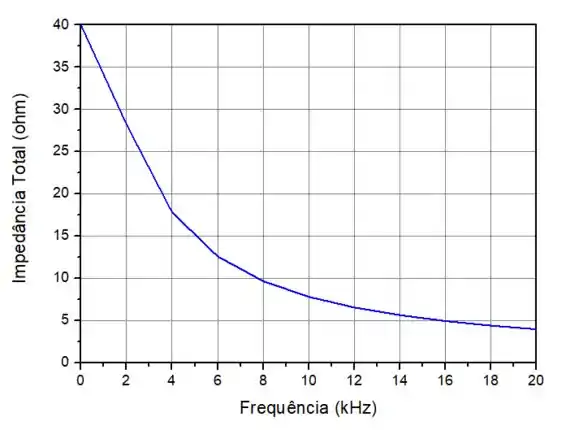
E:
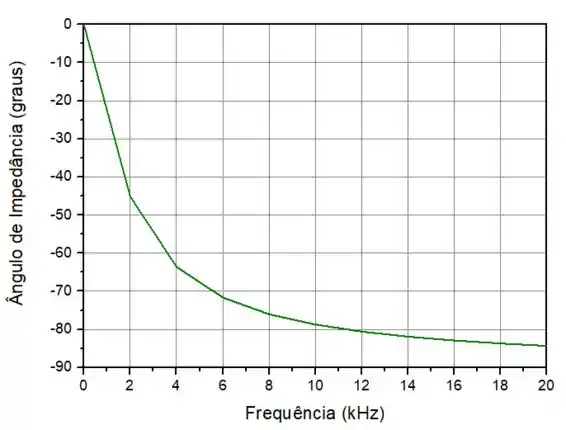
Passo 4
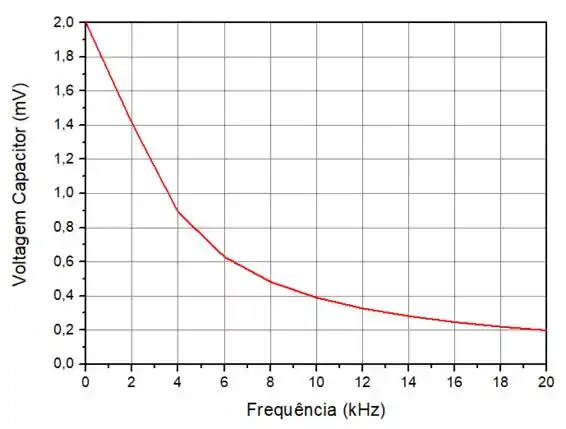
Para o item (b) queremos o gráfico da tensão no capacitor em função da frequência.
Podemos observar que temos um circuito em paralelo, por isso a tensão no capacitor é a mesma que a tensão na impedância total.
Esta calculamos a partir da seguinte fórmula:
Logo:
Substituindo os valores, temos que:
Abaixo, temos o gráfico desta equação no intervalo solicitado:
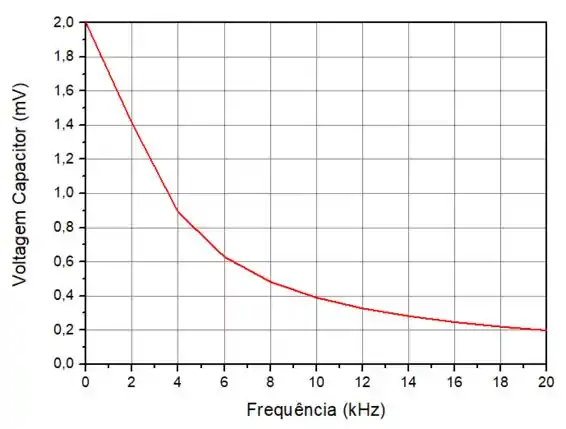
Passo 5
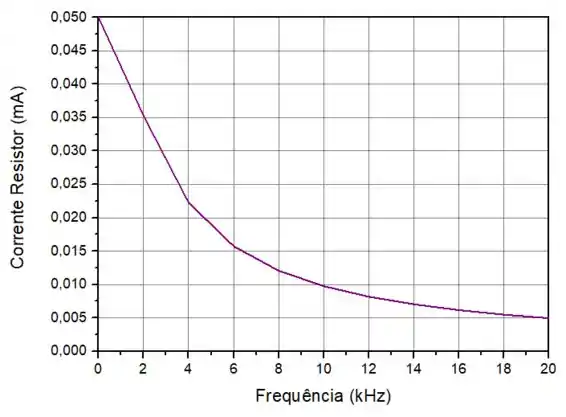
Para o item (c) queremos o gráfico da corrente do resistor em função da frequência.
A corrente que flui através da resistência é dada por:
Substituindo os valores, temos que:
Abaixo, temos o gráfico desta equação no intervalo solicitado:
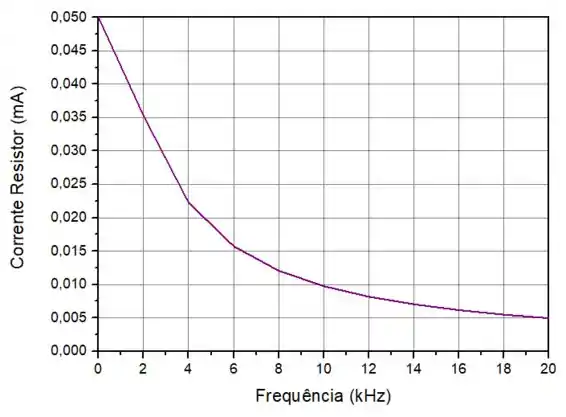
Opa, resolvida... Agora vamos para a próxima!!
Resposta