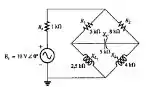
Para o circuito em ponte visto na figura 17.79:
a. A ponte está equilibrada?
b. Usando a análise de malhas, determine a corrente na reatância capacitiva.
c. Usando a análise nodal, determine a tensão na reatância capacitiva.
Passo 1
Faaala, galerinha!! Bora resolver juntos essa questão??
Bom, antes de tudo, precisamos entender se a ponte está balanceada. Para que ela esteja, a igualdade entre Z1/Z3 e Z2/Z4 deve ser verdadeira, certo? Vamos juntos confirmar isso:
Bom, como encontramos uma igualdade verdadeira, podemos dizer que sim! A ponte está sim balanceada. Bora juntos pra letra b.
Passo 2
Na letra b, precisamos relembrar as equações de uma ponte. Nós temos que:
(1)
(2)
Bom, podemos perceber que temos 3 equações pra 3 incógnitas, certo?
Vamos substituir os valores que já temos pra isso ficar mais claro pra nós:
(1)
(2)
Prontinho! Agora, nos resta resolver esse sistema, encontrando que:
Assim, encontramos que a corrente na reatância é 0A. Bora pensar um pouquinho na letra c.
Passo 3
Aqui, na letra c, queremos encontrar a tensão na reatância capacitiva. Bom, como tivemos que não há corrente, conseguimos supor aqui, que a tensão também será 0, certo? Assim, podemos dizer que a tensão na reatância capacitiva é nula, igual a 0V.
Resposta
a. Sim.
b.
c.