Para o circuito visto na Figura 10.107, considere i instante de tempo de 100ms após o fechamento da chave (posição 1) e determine:
a)
b)
c)
d)
e) Se a chave for colocada na posição 2 uma hora mais tarde, qual será o tempo necessário para que Vr2 caia para 20 V?
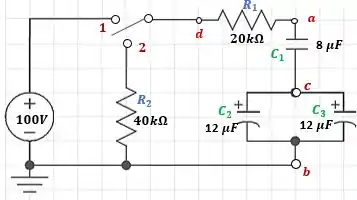
Figura 10.107
Passo 1
E aí galerinha?! Vamos resolver mais uma questão de circuitos RC.
a) Podemos simplificar um pouco o circuito, calculando a capacitância equivalente entre e , pois não tem ponto nenhum entre eles, que prejudique a análise quando unidos. Então será:
Vamos fazer mais uma contração, para que possamos calcular a constate de tempo do circuito. Essa contração será o cálculo da capacitância total.
Passo 2
Como a chave está inicialmente ligada ao terminal 1, o que irá vale para o cálculo da constante de tempo, será somente a malha externa. Sendo assim, temos:
Assim temos a expressão para , sendo:
Passo 3
Para um tempo t= 100 ms, temos:
Como o está compreendido entre os pontos a e b, temos:
Passo 4
b) A tensão sobre os pontos a e c, corresponde a tensão sobre o capacitor . Como está em série com , a carga sobre ambos é igual a carga de . Como já possuímos a tensão sobre , podemos calcular a carga como:
Isso implica em:
Assim podemos calcular a tensão sobre
Passo 5
c) A tensão sobre os pontos c e b, corresponde a tensão sobre , como já sabemos a carga desse capacitor, a tensão corresponderá:
Passo 6
d) A tensão sobre os pontos a e d, corresponde a tensão sobre , que pela lei das malhas, será expresso por:
Logo,
Então:
Passo 7
e) Se a chave for colocada na posição 2 uma hora mais tarde, qual será o tempo necessário para que Vr2 caia para 20 V?
Com a chave na posição 2, temos um circuito com uma única malha, porém com dois resistores em série, como mostrado abaixo:
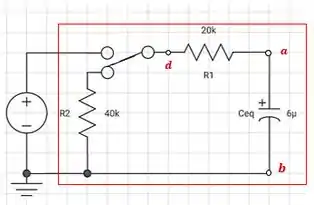
Para simplificar nossa analise, vamos expressar no circuito a capacitância total. Como a resistência do circuito mudou, a constante de tempo também se altera, então temos que determinar a nova constante.
Para determinar o tempo com que a tensão em seja 20 V, vamos utilizar uma das leis de Kirchhoff, onde a soma da tensão em cada um dos componentes tem que ser igual a zero. O que nos indica que:
Utilizando a primeira lei de Ohm, podemos escrever a tensão como o produto da corrente por resistência, assim temos:
Sendo o valor de a metade de , podemos escrever:
assim podemos colocar o em evidência:
voltando a olhar esse produto como tensão, temos:
Como sabemos a tensão da fonte (que carregou o capacitor) e a nova constante de tempo, só nos falta encontrar o tempo.
assim teremos:
Resposta
a)
b)
c)
d)
e)