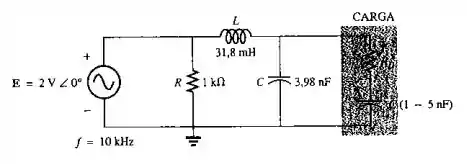
a. Para o circuito visto na Figura 18.132, calcule o valor da capacitância que garante uma potência máxima na carga se a capacitância está limitada à faixa de 1nF à 5nF.
b. Usando os resultados do item (a), determine o valor de para garantir uma potência máxima na carga.
c. Usando os resultados dos itens (a) e (b), determine a potência máxima na carga.
Passo 1
E aí, pessoal? Suave? Vamos resolver mais um exercício de circuitos.
Primeiro, vamos chamar a impedância da carga que substitui o capacitor de . Lembre-se que a máxima transferência de potência para carga ocorre quando , isto é, devemos obter o circuito equivalente de Thévenin para o circuito externo à carga .
Vamos listar as impedâncias desse circuito, externas a carga. Note que primeiro devemos
Passo 2
Vamos começar por . Desligando a fonte , obtemos um curto circuito em seu lugar. Como a impedância fica em paralelo com um curto circuito, teremos apenas uma associação em paralelo entre e em paralelo, de modo que:
Assim, e
Como , .
Como a potência máxima fornecida à carga é de e , não podemos determinar o resultado pedido pelo enunciado.
Resposta
a.
b.
c. Indeterminada