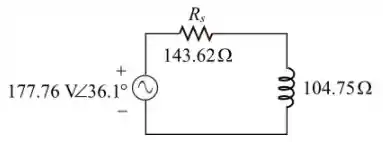
Para o circuito visto na Figura :
- Calcule , e em forma fasorial.
- Calcule o fator de potência total indicando se ele é atrasado ou adiantado.
- Calcule a potência média fornecida ao circuito.
- Construa o diagrama de admitâncias.
- Construa o diagrama de fasores para as correntes , e e a tensão .
- Determine a corrente nos capacitores usando apenas a lei de Kirchhoff para correntes.
- Determine um circuito em série com um elemento resistivo e outro reativo que tenha a mesma impedância que o circuito original.
Passo 1
Opa pessoal, tudo certinho aí? Vamos resolver esta questão.
A admitância total do circuito do enunciado é dado por:
Susbtituindo os valores, temos que:
Agora, vamos calcular a impedância total:
Agora vamos calcular a corrente que flui através do resistor:
E a corrente através do indutor:
Passo 2
Para o item (b) temos que calcular o fator de potência total.
Temos que a voltagem da fonte vale:
Portanto seu fator de potência é dado por:
Passo 3
Para o item (c), temos que calcular a potência média entregue à linha:
Calculando, temos que:
Passo 4
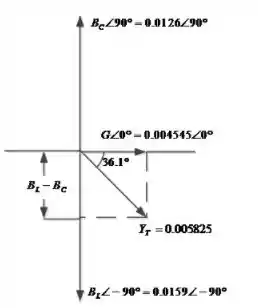
O item (d) nos pede um desenho do diagrama de admitância. Segue abaixo um esboço:
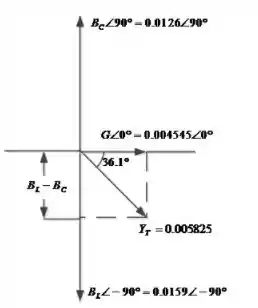
Passo 5
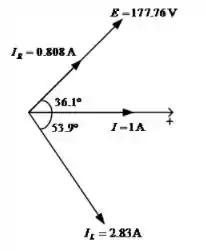
Para o item (e), nos é solicitado o diagrama de fasores para as correntes. Segue abaixo um esboço:
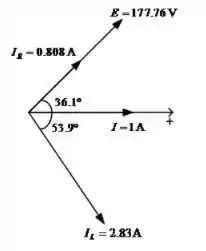
Passo 6
Para o item (f), queremos calcular a corrente nos capacitores, usando a lei de Kirchhoff. Temos que:
Portanto, a corrente no capacitor será:
Passo 7
Para o item (g), temos que esboçar um circuito em série com um elemento resistivo e outro reativo e que possua a mesma impedância total do sistema original.
Já descobrimos, no item (a) que a impedância total, vale:
Portanto, o circuito alternativo em série, poderia ser representado da seguinte maneira:
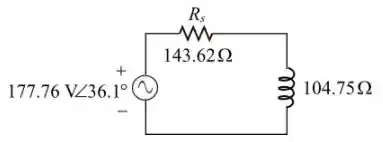
Resposta