Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Introdução a Análise de Circuitos, de Boylestad- Ed: 10º - Capítulo 16.Problemas - Ex. 2

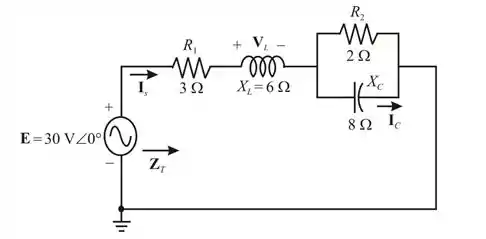
Para o circuito visto na Figura 16.40:

  1. Determine a impedância total Z T .
  2. Determine a corrente I s ' .
  3. Calcule   I C usando a regra dos divisores de corrente.
  4. Calcule V L usando a regra dos divisores de corrente.

Passo 1

E ai galerinha, tudo na paz??

Então bora que bora

Consideremos o diagrama de circuito mostrado a seguir:

Passo 2

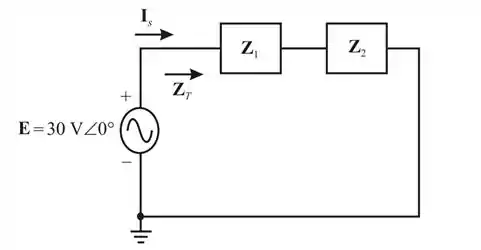
  1. Para encontrarmos a impedância total Z T , vamos considerar o circuito mostrado a seguir .

    2. Passo 3

    Partindo do circuito mostrado no passo anterior, a impedância Z 1 é a combinação em série de R 1   e   X L , e Z 2 é a combinação paralela de R 2   e   X C .

    Calculando a impedância Z 1

      Z 1 = R 1 + j   X L

    Z 1 = R 1 ∠ 0 ° + X L ∠ 90 °

    Z 1 = 3 Ω ∠ 0 ° + 6 Ω ∠ 90 °

    Z 1 = 6.7   ∠ 63.43   Ω

    Calculando a impedância Z 2

    Z 2 = ( R 2 ) ( - j X C ) R 2 - j X C

    Z 2 = ( 2 Ω ∠ 0 ° ) ( 8 Ω ∠ - 90 ° ) 2 Ω - j 8 Ω

    Z 2 = 16   Ω ∠ - 90 ° 8.25 Ω ∠ - 75.96

    Z 2 = 1.94   Ω ∠ - 14.04 °

    Passo 4

    A impedância total Z T é

    Z T = Z 1 + Z 2

    Z T = 6.7   Ω ∠ 63.43 ° + 1.94 Ω ∠ - 14.04 °

    Z T = 2.99 + j 5.99 + 1.88 - j 0.47

    Z T = 4.87 + j 5.52 Ω

    Z T = 7.36 ∠ 48.58 ° Ω

    Portanto, a impedância total Z T da rede dada é 7.36 ∠ 48.58 ° Ω .

    Passo 5

  2. A fonte atual I S é,

    3. I S = E Z T

    I S = 30   V   ∠ 0 ° 7.36 ∠ 48.58   °   Ω

    I S = 4.076   A   ∠ - 48.58 °

    Portanto, a fonte de corrente I S é 4.076   A   ∠ - 48.58 ° .

    Passo 6

  3. Aplique a regra do divisor atual para encontrar a atual I C .

    4. I C = R 2 R 2 - j X C I S

    I C = R 2 ∠ 0 ° R 2 ∠ 0 ° + X C ∠ - 90 ° I S

    I C = 2 Ω ∠ 0 ° 2 Ω ∠ 0 ° + 8 Ω ∠ - 90 ° 4.076   A   ∠ - 48.58 °

    I C = 2 Ω ∠ 0 ° 2 Ω + j 8 Ω 4.076   A   ∠ - 48.58 °

    I C = 2 Ω ∠ 0 ° 8.25 Ω ∠ - 75.96 ° 4.076   A   ∠ - 48.58 °

    I C = 0.24 ∠ 75.96 ° 4.076   A   ∠ - 48.58 °

    I C = 0.877 + j 0.454

    I C = 0.978 ∠ 27.38 °

    Portanto, o atual I C é de 0.978 ∠ 27.38 ° .

    Passo 7

  4. Aplicando a regra do divisor de corrente de tensão para encontrar a corrente V L .

V L = j X L R 1 + j X L + Z 2 ( E )

V L = j X L Z 1 + Z 2 ( E )

Substituindo

V L = j 6 6.7 Ω ∠ 63.43 ° + 1.94 Ω ∠ - 14.04 ° 30   V   ∠ 0 °

V L = 6   ∠ 90 ° 6.7 Ω ∠ 63.43 ° + 1.94 Ω ∠ - 14.04 ° 30   V   ∠ 0 °

V L = 180   ∠ 90 ° 2.99 + j 5.99 + ( 1.88 - j 0.47 )

V L = j   180 4.87 + j   5.52

V L =   180 ∠ 90 ° 7.36 ∠ 48.58 °

V L = 18.34 + j 16.18

V L = 24.45   V   ∠ 41.42 °

Assim, a tensão V L é 24.45   V   ∠ 41.42 ° .

Resposta

Ei, a resposta está no passo a passo :)