Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Introdução a Análise de Circuitos, de Boylestad- Ed: 10º - Capítulo 16.Problemas - Ex. 4

Para o circuito visto na Figura 16.42:

  1. Determinar a impedância total Z T .
  2. Calcule a tensão V 2 e a corrente I L .
  3. Calcule o fato de potência do circuito.

Passo 1

E ai galera, so vamoo??

Partiuuu!!

  1. Consulte a figura 16.42 no livro, logo após vamos escrever a equação para encontrarmos a impedância.

    2. Z 1 = 2   Ω

    Z 2 = - j   4 Ω | | (   j 6 Ω )

    Z 2 = - j   4 Ω (   j 6 Ω ) - j   4 Ω + (   j 6 Ω )

    Z 2 = - j   4 Ω (   j 6 Ω ) j 2 Ω

    Z 2 = 12 Ω   ∠ - 90 °

    Z 3 = ( 8 Ω | 8 Ω | | ( j 3 Ω )

    Z 3 = 4 Ω | | ( j 3 Ω )

    Z 3 = 4 Ω ( j 3 Ω ) 4 Ω + ( j 3 Ω )

    Z 3 = 2.4 Ω   ∠ 53.13 °

    Passo 2

    Redesenharemos a fig 16.42 para determinarmos a impedância total. A rede modificada é mostrada a seguir.

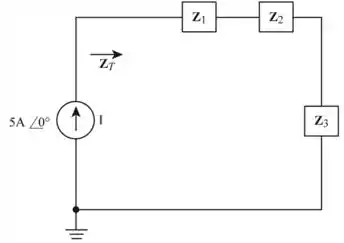
    Passo 3

    Consideraremos a seguinte expressão para podermos encontrar a impedância total para a rede fornecida.

    Z T = Z 1 + Z 2 + Z 3

    Substituindo

    Z T = 2 Ω + 12 Ω ∠ - 90 ° + ( 2.4 Ω ∠ 53.13 ° )

    Z T = 10.65 Ω   ∠ - 71.16 °

    Assim, a impedância total para a rede dada é   10.65 Ω   ∠ - 71.16 ° .

    Passo 4

  2. Considere a seguinte fórmula para encontrar a tensão ( V 2 ) .

    3. V 2 = Z 3 I

    Substituindo

    V 2 = ( 2.4 Ω ∠ 53.13 ° ) ( 5   A   ∠ 0 ° )

    V 2 = 12   V ∠ 53.13 °  

    Portanto o valor de V 2 é 12   V ∠ 53.13 °   .

    Passo 5

    Consulte a figura 16.41 no livro, e vamos escrever a seguinte fórmula para encontrar a corrente I L utilizando a regra do divisor de corrente.

    I L = ( 8 Ω | 8 Ω I ( 8 Ω | 8 Ω + j 3 Ω

    I L = 4 Ω I 4 Ω + j 3 Ω

    Substituindo

    I L = 4 Ω ( 5   A   ∠ 0 ° ) 4 Ω + j 3 Ω

    I L = 20   A   ∠ 0 ° 4 Ω + j 3 Ω

    I L = 4   A ∠ - 36.87 °

    Portanto, o valor da I L é de 4   A ∠ - 36.87 ° .

    Passo 6

  3. Considere a seguinte expressão para encontrarmos o fator de potência da rede.

F P = R Z T

Substituindo

F P = 3.44   Ω 10.65   Ω

F P = 0.323   ( p r i n c i p a l )

Portanto, o fator de potência é devido à carga capacitiva. Assim, o fator de potência da rede é de 0.323   ( p r i n c i p a l ) .

Resposta

Ei, a resposta está no passo a passo :)