Para o circuito visto na Figura :
- Determine a impedância total e a admitância total .
- Determine as correntes , e .
- Verifique a lei de Kirchhoff para correntes demonstrando que
- Determine o fator de potência do circuito e indique se ele é atrasado ou adiantado.
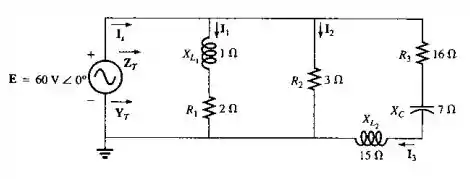
Passo 1
Opa pessoal, tudo certinho aí? Vamos analisar esta questão.
Podemos dividir o nosso circuito para três impedâncias. Temos que:
Para , temos que:
E para , temos que:
Passo 2
A impedância total, será:
A admitância total será:
Passo 3
Para o item (b) queremos as correntes.
Temos que:
Para , temos que:
E para , temos:
Passo 4
Portanto, a fonte da corrente será:
Passo 5
O fator de potência é dado por:
Portanto:
Consegui te ajudar? Responde Aí.
Resposta