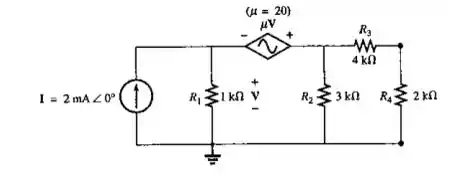
Para o circuito visto na Figura 18.127, obtenha o circuito equivalente de Norton para parte externa ao resistor de .
Passo 1
E aí, pessoal? Vamos resolver mais uma questão de circuitos juntos!
Primeiro, vamos listar as impedâncias do circuito. Podemos ignorar o resistor de pois estamos interessados no circuito externo ao mesmo.
Beleza, estamos prontos para descobrirmos os valores de corrente e impedância equivalentes de Norton para este circuito.
Passo 2
Iremos partir do equivalente de Thévenin para chegar no de Norton. Para isso, devemos substituir por um circuito aberto e analisar seus terminais.
Primeiramente, note que a tensão de Thévenin é a mesma sobre (a corrente em é nula). Chamando esta tensão de , temos que:
Observe também que a corrente da fonte se divide em duas correntes:, na impedância e , para o resto do circuito. Note que:
e
Assim, obtemos:
Passo 3
Em seguida, vamos determinar a corrente equivalente de Norton. Para isso, devemos substituir por um curto circuito e obter a corrente na impedância . Como e ficarão em paralelo, eles terão a mesma tensão, ou seja:
Vimos no passo 2 que é a tensão sobre a impedância e que a corrente da fonte se divide entre e os demais componentes do circuito. Isto é:
e
Já temos e , precisamos calcular . Podemos utilizar o seguinte divisor de corrente:
Assim, obtemos:
Logo, a impedância equivalente de Norton será dada por: