Para o circuito visto na Figura
a) Se a frequência de atenuação for e de transmissão, , determine os valores de para uma capacitância de
b) Trace a curva de resposta do circuito do item (a).
Passo 1
Oi galerinha, tudo bem?
Vamos juntos resolver mais um exercício!
a) Antes de começar teremos que lembrar de algumas relações que serão uteis na resolução desse exercício, beleza!
Para encontra a frequência de atenuação usaremos a relação:
Ei! A questão já lhe fornece e
Vamos Isolar para encontrar os valores de :
Substituindo os valores, teremos:
Agora vamos precisar encontrar a reatância do filtro para encontrar a frequência de transmissão, beleza!
Bora lá então!
Só lembrando que a reatância indutiva é:
Substituindo os valores:
Tranquilo até aí?

Agora vamos encontrar a reatância capacitiva, cuja a relação está descrita abaixo:
Substituindo os valores, teremos:
Como o valor da impedância indutiva é muito menor que a capacitiva, considerarei:
Logo:
Substituindo os valores:
Ufa, essa foi longa!
Temos ainda o próximo item

Passo 2
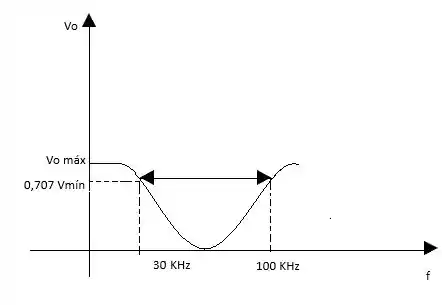
b) O esboço do gráfico para esse filtro está abaixo:
Lembrando que esse é um gráfico bem genérico para um filtro de banda dupla, para mais detalhe deve-se transformar o eixo das frequência para escala logarítmica, Tranquilo!
Ufa! Esse exercício chegou ao fim!
Vamos para o próximo
Resposta
a) ;
b)