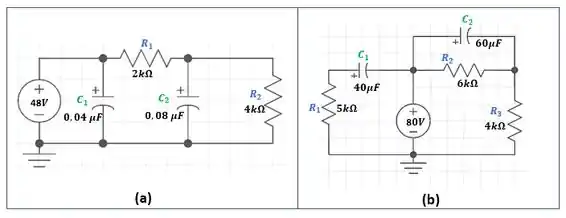
 Para os circuitos mostrados na Figura 10.106, determine a tensão entre os terminais de cada capacitor e suas cargas após atingirem seu valor final.
Para os circuitos mostrados na Figura 10.106, determine a tensão entre os terminais de cada capacitor e suas cargas após atingirem seu valor final.
Figura 10.106
Passo 1
Fali aí pessoal, prontos para mais um probleminha de circuitos elétricos?
Como de costume para essa seção, vamos anotar a relações importante para a questão

Passo 2
Para quem está chegando agora nesta seção, não deixe de conferir nos problemas 45 e 46, pois vamos nos basear na mesma análise. É importante que vocês façam o desenho para visualizar melhor as reduções dos circuitos, assim como fizemos nas questões 44 e 45.
a) Como está paralelo a fonte, a tensão sobre ele é a mesma da fonte:
Com isso, sua carga é expressa por:
Passo 3
Como e estão em paralelo, a tensão sobre eles vai ser a mesma, logo só precisamos determinar a tensão sobre o resistor.
Com isso, sua carga é expressa por:
Passo 4
b) Neste item, temos , logo a tensão sobre eles é a mesma. Então podemos calcular a tensão sobre , onde:
Logo,
Com isso, sua carga é expressa por:
Passo 5
Agora ao analisarmos a malha a esquerda, podemos calcular a tensão sobre o resistor.
O que indica que a tensão sobre o capacitor deve ser:
Com isso, sua carga é expressa por:
Resposta
a) ; ; ;
b) ; ;