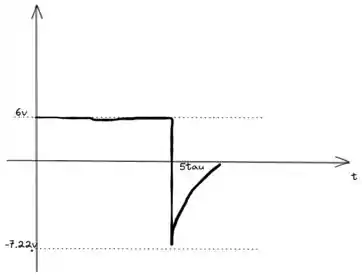
Considerando o circuito da Figura 12.75:
a) Escreva uma a expressão matemática para a corrente e a tensão quando a chave é fechada.
b) Determine as expressões matemáticas para e se a chave for aberta após se passarem cinco constantes de tempo.
c) esboce as formas de onda para os itens (a) e (b) no mesmo gráfico.
d) Esboce a forma de onda para a tensão em R2 para o intervalo estabelecido no item anterior.
Passo 1
Bora bora, mais exercício! Vamos começar esse exercício diferente? Vamos começar redesenhando o circuito para facilitar nossa análise, pois do jeito que ele tá desenhado é um pouquinho confuso.
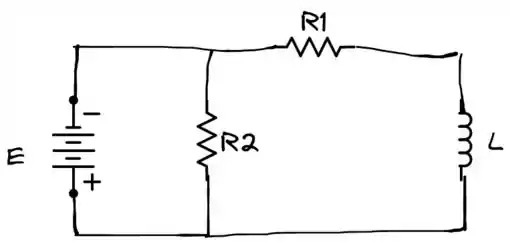
Com o circuito redesenhado fica mais fácil de interpretar o problema, né? Vamos fazer o equivalente de thévenin para facilitar ainda mais pra gente. Vamos calcular Rth (lembrando que calculamos com a chave fechada). Olhando dos terminais do indutor, , pois o resistor R2 fica paralelo com um curto circuito, ou seja, fora da jogada. Assim:
Agora para descobrirmos o Vth ficou fácil! Já que temos o R2 em paralelo com a fonte, a tensão Vth é a tensão em cima de R2, ou seja, a própria fonte! mole!
Agora já conseguimos calcular o conhecendo a resistência e a indutância:
Bora calcular a tensão agora no próximo passo!
Passo 2
Vamos escrever a expressão de corrente para os indutores. Como neste caso não há corrente inicial basta usar a equação mais simples:
Substituindo os valores que conhecemos:
Para calcular a tensão é a mesma coisa. Vamos escrever a fórmula da tensão:
Já conhecemos todas as variáveis então é só reescrever:
Mole né? Bora que tem mais 3 letras pra fazer ainda
Passo 3
Abrindo a chave, o indutor descarrega através de R1 e de R2, ou seja, vamos ter que recalcular o :
Agora é só jogar nossos valores na equação da descarga da corrente e da tensão. Vamos começar pela da corrente e substituir os valores que conhecemos (lembrando que a corrente é a mesma e o a gente recalculou):
Pronto, temos a corrente. Agora vamos escrever a equação da tensão na descarga e substituir os valores:
Matamos o problema! Agora só falta desenhar:
Passo 4
Esboçando os 2 gráficos com os valores que conhecemos fica assim:
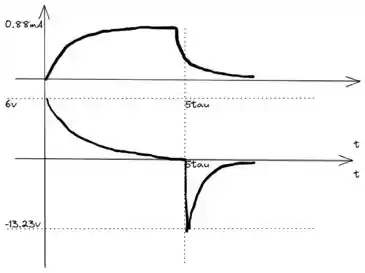
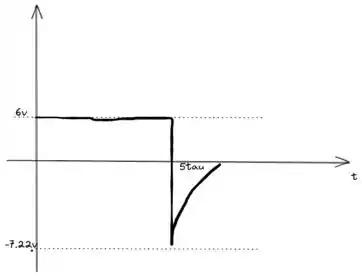
Resposta
a)
b)
c)
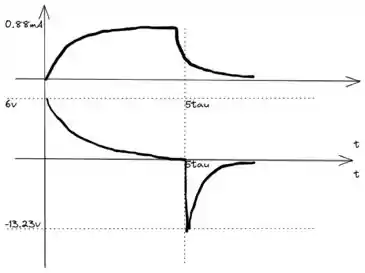
d)