Considerando o circuito da Figura 12.76:
a) Determine as expressões matemáticas para a corrente e a tensão quando a chave é fechada.
b) Repita o item (a) se a chave for fechada em
c) esboce as formas de onda para os itens (a) e (b) no mesmo gráfico.
Passo 1
Mais exercício de indutor! Nesse não vamos precisar de equivalente de thévenin. Vamos começar calculando o direto? Lembrando que o indutor vai se carregar apenas através de R1:
Feito! Agora basta a gente usar as equações da tensão e corrente na carga. Primeiro a da corrente:
Substituindo os valores que conhecemos:
Para calcular a tensão é a mesma coisa. Vamos escrever a fórmula da tensão:
Já conhecemos todas as variáveis então é só reescrever:
Mole mole, bora pra próxima parte!
Passo 2
Precisamos recalcular a corrente para antes de abrirmos a chave. Vamos escrever a equação da corrente nessa situação e substituir o :
Agora sim podemos abrir a chave! Abrindo a chave, o indutor descarrega através de R1 e de R2, ou seja, vamos ter que recalcular o :
Agora é só jogar nossos valores na equação da descarga da corrente e da tensão. Vamos começar pela da corrente e substituir os valores que conhecemos (lembrando que a corrente é que a gente calculou para e o a gente recalculou para a descarga):
Pronto, temos a corrente. Agora vamos escrever a equação da tensão na descarga e substituir os valores:
Matamos o problema! Agora só falta desenhar
Passo 3
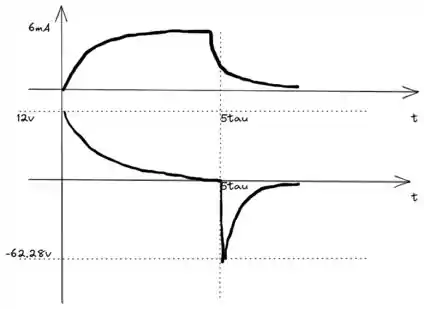
Esboçando os 2 gráficos com os valores que conhecemos fica assim:
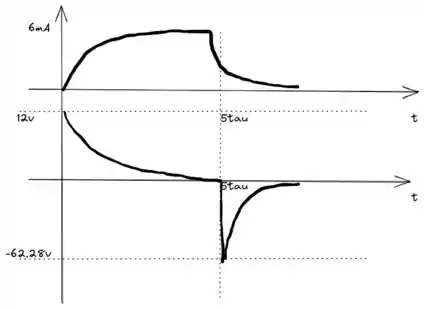
Resposta
a)
b)
c)