Considere o circuito da figura P 3.2-3.
a) Suponha que e . Determine a corrente e a tensão .
b) Em vez disso, suponha que e . Determine as resistências e .
c) Em vez disso, suponha que a fonte de tensão fornece uma potência de e que a fonte de corrente fornece uma potência de . Determine a corrente , a tensão e as resistências e .
Passo 1
a) Faala, galera! Bora pra mais uma. Aqui para este primeiro item, podemos usar as Leis de Kirchhoff para encontrar algumas relações que podem nos ajudar a resolver o problema.
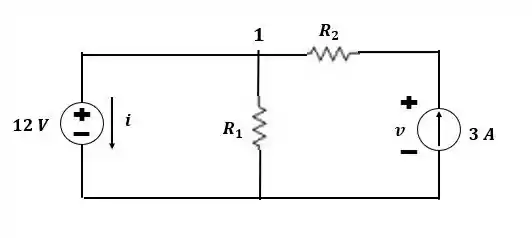
Primeiro aplicaremos a LKC ao nó 1:
Com R1 = 8 :
Aplicando a LKT ao laço que engloba as duas malhas:
Com R2 = 4 :
Passo 2
b) Agora poderemos reutilizar as relações (1) e (2) encontrados na letra (a) e aplicar os novos valores fornecidos:
Aplicando i = 2.25 na relação (1):
Aplicando v = 42 V na relação (2), teremos:
Passo 3
c) Agora, primeiramente, utilizaremos a fórmula da potência para determinar os novos valores de i e v já que o enunciado nos forneceu as potências desses elementos:
Para calcular o novo valor de i, teremos que:
Com P = 24 W:
Agora calcularemos o novo valor de v, utilizando novamente a fórmula da potência:
E, por fim, utilizando as relações (1) e (2), encontraremos os novos valores de R1 e R2:
Utilizando a relação (1):
Com i = -2 A:
Utilizando a relação (2), teremos:
Com v = 3 V:
Aqui encontramos um valor negativo para o resistor R3, o que significa que a situação descrita no enunciado não é possível!
Aqui finalizamos a questão, galera. Até a próxima! 😊
Resposta
a)
b)
c)