Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 15

Considere o circuito na figura e calcule o valor de necessário para que a resposta seja criticamente amortecida.

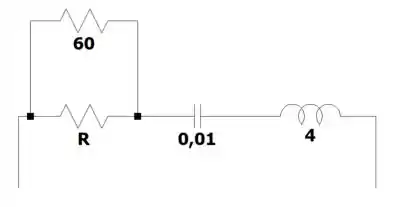
Passo 1

Pra facilitar nossa vida, antes de tudo vamos transformar o resistores e o de em um só, tipo assim:

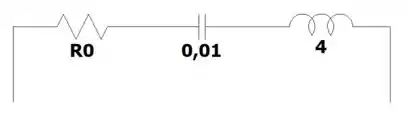
Transformando nosso circuito pro domínio :

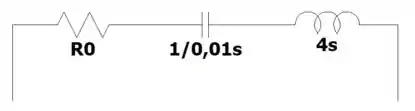
Passo 2

Do circuito, podemos escrever:

Somando os termos:

Pra analisar quando o circuito vai ser criticamente amortecido, temos que analisar as raízes de certo? E pra ser criticamente amortecido elas devem ser iguais :)

Passo 3

As raízes de , por Bhaskara, são dadas por:

Queremos que o circuito tenha resposta criticamente amortecida, ou seja, que suas raízes sejam iguais.

Pra que suas raízes sejam iguais, deve ser igual a 0, certo?:

Boaa, achamos o valor de que torna o circuito criticamente amortecido, mas a gente quer o valor de não é?

Passo 4

Definimos como:

Então, para o circuito ser criticamente amortecido, devemos ter:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave do tipo liga-antes-interrompe-depois no circuito da Figura P13.39 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Determine i o , para t ≥ 0.

Não há nenhuma energia armazenada no circuito da Figura P13.25, no instante em que a chave é fechada. a) Determine v o , para t ≥ 0. b) Sua solução faz sentido em termos do comportamento conhecido do

Não há nenhuma energia armazenada no circuito na Figura P13.31 no instante em que a fonte de corrente é aplicada. a) Determine Ia e Ib. b) Determine ia e ib. c) Determine Va, Vb e Vc. d) Determine va,

Não há nenhuma energia armazenada no circuito da Figura P13.27, no instante em que a fonte de corrente é ligada. Dado que i g = 100u(t) A: a) Determine Io(s). b) Use os teoremas dos valores inicial e