(a) Considere duas cargas pontuais , separadas por uma distância de . Construa o plano equidistante das duas cargas. Integrando o tensor das tensões de Maxwell sobre esse plano, determine a força de uma carga sobre a outra.
(b) Faça o esmo para cargas com sinais opostos.
Passo 1
Falaaa, meu querido/ minha querida!! As cargas e as forças agindo sobre o ponto que queremos entrar a Força total, podem ser analisadas abaixo:
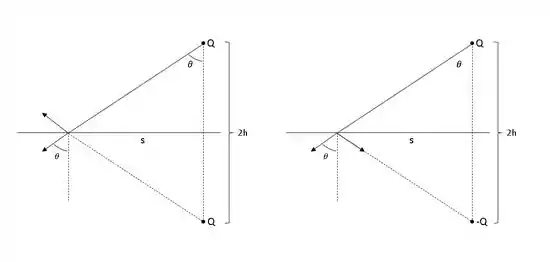
A figura a esquerda representa a letra (a) e a direito a (b). Bora para os cálculos!!!
Passo 2
Na figura da esquerda, o campo elétrico é dado por:
Onde, , logo:
Com o elemento de superfície sendo , a força será na direção .
Logo, só teremos a componente . E a força magnética fica:
Portanto, achamos o mesmo resultado que acharíamos usando a lei de Coulomb.
Passo 3
Para a parte direita da figura, a força no plano será em negativo, teremos de novo apenas . O campo elétrico é:
Onde
Calculando a força:
Terminamos!!!