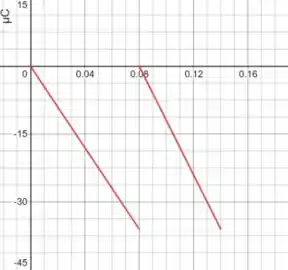
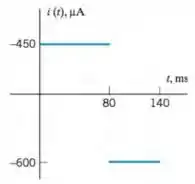
A corrente em um componente de um circuito está plotada em função do tempo na figura P 1.3-5. Plote a carga que atravessa o fio em função do tempo .
Passo 1
Eaí galera, bora iniciar mais uma questãozinha com a gente!
Essa questão é simples, mas requer atenção na análise do gráfico.
As funções que definem o gráfico são dadas por:
Por definição a formula da carga elétrica nos diz que:
Com isso a gente pode calcular a carga em cada intervalo de tempo.
Tudo certinho, agora vem comigo na resolução!
Passo 2
Calculando a carga para:
:
:
:
Com isso, temos o as seguintes funções nos intervalos de tempo:
Plotando o gráfico da função, temos o seguinte resultado: