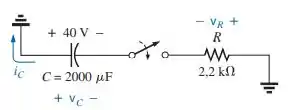
Figura 10.86
Passo 1
Olá pessoal! Mas um probleminha para alegrar o dia 😄.
Diferente dos problemas anteriores, o capacitor já está incialmente carregado. Então a diferença de potencial desse circuito é a indicada pelo capacitor.
Com isso, vamos anotar as informações do problema:
Passo 2
Para escrever as expressões solicitadas no enunciado, é preciso encontrar a constante de tempo, como fizemos nos últimos exercícios, dada por:
Sendo assim, temos:
Passo 3
A atenção nesta etapa deve se focar na expressão utilizada, sendo para o processo de descarga, descrita como:
Inserindo as informações que o problema apresenta, temos:
E para esse caso, temos , logo:
A maior parte nós já resolvemos 🤩
Passo 4
A equação que expressa a corrente no processo de descarga é dada por:
Inserindo as informações que o problema apresenta, temos:
Pronto! Não foi tão difícil assim 😃