É dado que no intervalo .a) Construa uma função periódica que seja igual a entre , tenha um periodo de metria de meia-onda.
b) A função é par ou ímpar?c) A função tem simetria de quarto de onda?d) Calcule a série de Fourier para .e) Calcule a série de Fourier para se for deslocada para a direita.
Passo 1
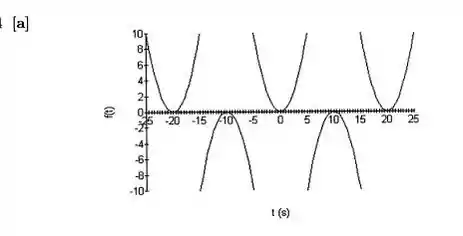
Passo 2
par
Passo 3
sim
Passo 4
par, simetria de meia onda
O primeiro termo é 0 em T/4 e 0; segundo termo é 0 em 0, portanto
Passo 5
Resposta
a. 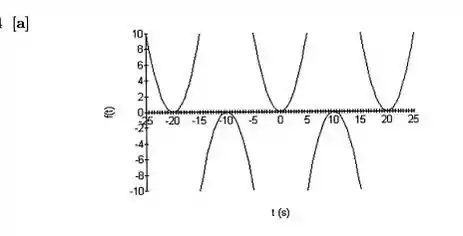
b. par
c. sim
d.
e.