Descreva com suas próprias palavras os efeitos da frequência sobre o funcionamento dos transformadores. Use o circuito equivalente aplicável e os efeitos de frequência que aparecem neste capítulo.
Passo 1
E aí galerinha, esse é um problema um tanto atípico, mas que já foi discutido na seção 21.7, então todas as equações e relações de proporcionalidade que vamos utilizar aqui, já foram mostradas e trabalhadas em outros problemas, e isso com certeza vai facilitar nossa vida.
A figura abaixo é a esquematização de um transformador ideal, com o qual vamos trabalhar.
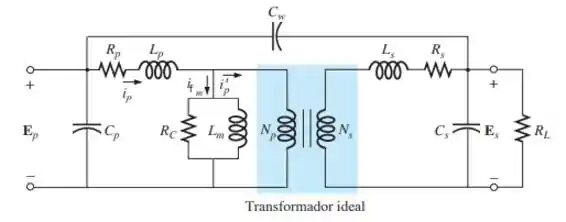
Vamos dividir nossa análise em faixas específica de frequência, para separarmos bem os efeitos.
- Baixa frequência
- Médias frequências
- Altas frequências
Neste caso, a reatância em série será proporcional a , e como a frequência é muito baixa, isso irá indicar que a reatância será muito pequena, ao ponto de podermos desconsiderá-la. Com isso e serão desprezadas.
Mas neste caso, não poderá ser desprezada, por estar em paralelo com o circuito refletido, mostrado abaixo no circuito equivalente. Onde as impedâncias refletidas do circuito secundário, são representadas no lado direito da ilustração.
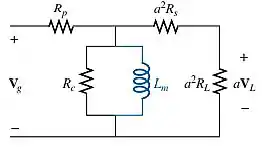
Mas vale lembrar, que mesmo sem desprezar , ele continua sendo proporcional a frequência, o que nos indica, que se reduzirmos a frequência ao máximo () vamos ter o como um curto circuito. Dessa forma, a corrente primária, irá passar toda pelo caminho de menor resistência, que é onde se encontro o , como mostrado abaixo:
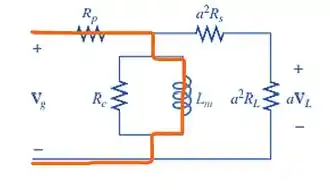
Isso o leva a um cenário onde a tensão no circuito secundário é nula. Então, quanto mais baixa a frequência, menor será a tensão .
Passo 2
Vamos olhar ainda para o circuito equivalente anterior.
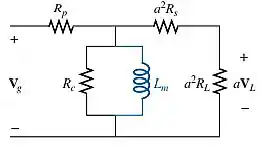
Quando aumentarmos a frequência (passar para uma ordem de grandeza diferente), a reatância de vai se tornar tão grande, comprada a impedância refletida, que não vai haver corrente neste trecho, o que nos permite excluir do circuito equivalente. Isso vai provocar uma tensão constante no circuito secundário. Assim, o circuito equivalente, neste caso, vai ter a forma de:
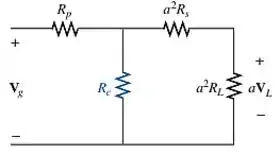
Passo 3
Para este caso, vamos retorna ao transformador ideal, pois as considerações que fizemos nos dois passos anteriores, não vão nos servir.
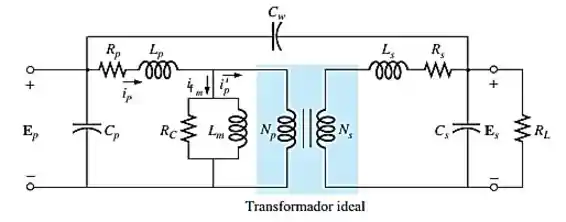
Neste caso as reatâncias e não serão descartadas por conta do fluxo residual (lembrando que em circuitos magnéticos temos a histerese).
Como estamos trabalhando com circuito reduzidos, vamos refletir o circuito secundário no primário. Assim, teremos:
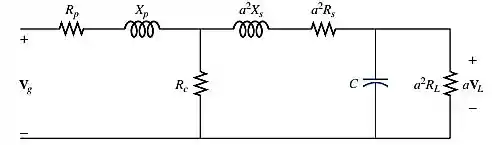
O não aparece neste circuito, pelo mesmo motivo anterior. C neste caso está representando e , enquanto será desconsiderado por seus efeitos serem muito menores quando comprados com os efeitos produzidos por C.
Então para as frequências altas, como essas que estamos explorando neste passo, a reatância capacitiva tem uma relação inversa com a frequência, como é expressa pela equação abaixo:
Isso nos deixa com a relação:
Isso nos diz, que quanto maior a frequência, menor será a reatância do capacitor, que o aproxima de um curto circuito, assim como no caso anterior, a corrente passará pelo caminho “mais livre” que encontrar.
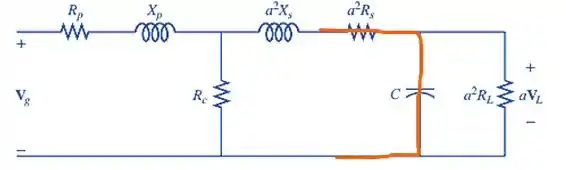
Isso no indica, que a tensão tende a diminuir, ao passo que a frequência atinge valores muito altos.
Resposta
Tudo que descrevemos aqui, pode ser expresso em um único gráfico, como o mostrado abaixo:
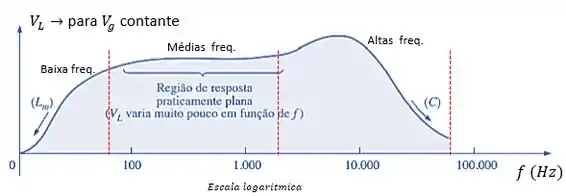
Assim, temos para baixa frequência um comportamento vinculado ao , indicado no lado esquerdo, onde diminui a tensão também diminui. Para médias frequências, temos uma resposta quase constante, por conta do alto valor de . E para frequências altas, dois comportamentos distintos, que aumenta com a frequência até o ponto onde a frequência se tonar tão alta, que a reatância do capacitor se torna baixa o suficiente para entrar em curto e a tensão despencar.