Desenhe o circuito equivalente de Norton para a parte de cada um dos circuitos vistos na Figura 9.135 externas ao ramo a-b.
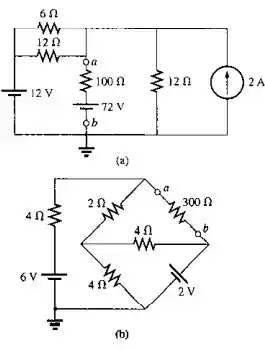
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Vamos redesenhar o circuito como mostra a figura a seguir (Figura 1), e iremos encontrar a resistência de Norton
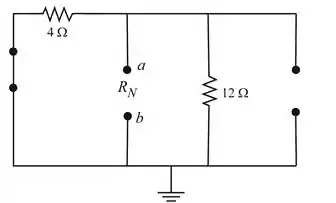
Vamos usar o método da superposição
Redesenhando o circuito como mostrado na Figura 2, e iremos encontrar a corrente de Norton
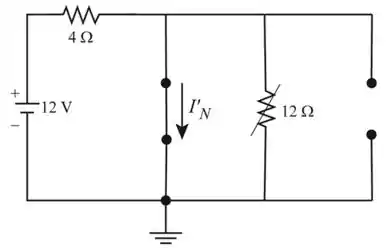
Aplicando a lei de Ohm e encontrando a corrente de Norton.
Redesenhando a figura, como mostra a figura 3, encontraremos a corrente de Norton
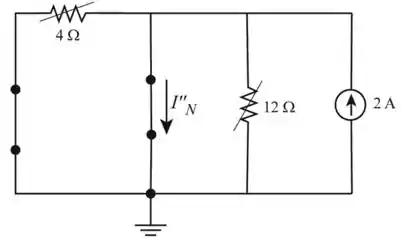
Calculando a corrente total de Norton
Portanto, o valor de É 5 A.
Desenharemos o circuito equivalente de Norton como mostrado na Figura 4
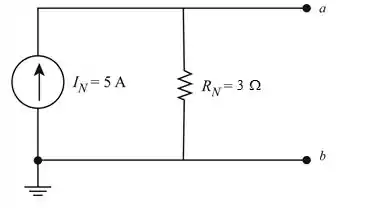
Passo 2
b. Vamos redesenhar como mostra a figura 5, e encontrar o valor da resistência de Norton
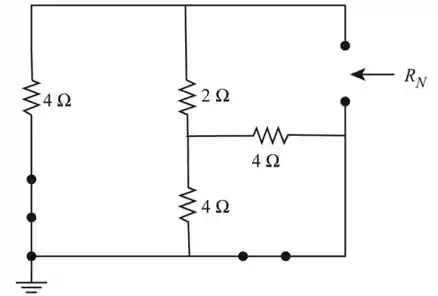
Encontraremos a resistência equivalente de Norton da rede
Redesenhando, como mostra a figura 6
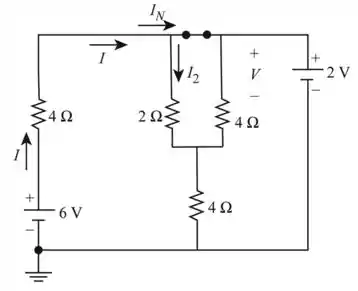
Passo 3
Aplicando a lei de Ohm iremos encontrar a corrente total no circuito
Aplicando a regra do divisor de tensão e iremos encontrar a tensão V na figura 6 .
Aplicando a lei de Ohm encontraremos na figura 6.
Calcularemos a corrente de Norton
Portanto, o valor
Desenhando o circuito equivalente do Norton como mostra a figura 7.
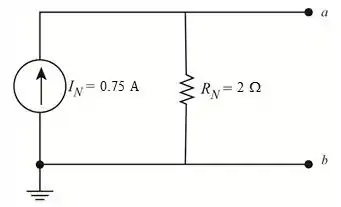
Resposta
- Figura 4.
- Figura 7.