a) Desenhe o circuito equivalente de thévenin para o circuito externo ao resistor R em cada um dos circuitos mostrados na Figura 9.128
b) determine a corrente em R para R igual a
Passo 1
Vamos fazer a letra a e b para o primeiro circuito nesse exercício para ficar bem separadinho! Bora começar a relembrar primeiro o passo a passo do teorema de thevenin:
1. Leve todas as fontes em 0, e calcule a resistência (Rth) à partir dos terminais avaliados
2. Volte com as fontes e descubra a tensão nos terminais avaliados (Vth)
3. Redesenhe o circuito com a tensão calculada e a resistência calculada.
Para levar a fonte de corrente a 0 é o contrário da fonte de tensão. Na de tensão a gente finge que ela não existe e a corrente passa toda por ela, né? na de Corrente ela vira um circuito aberto e não passa nenhuma corrente por ela! Dito isso já conseguimos resolver nosso problema da letra a) fazendo o passo a passo do thevenin
Vamos começar calculando Rth. Olhando pelos terminais de R, R1 está em série com R2, e só! Vamos escrever a equação e calcular
Mole demais esse Rth né? bora pro Vth agora
Passo 2
Vamos agora voltar com a fonte de corrente e calcular a tensão nos terminais de R. Conseguimos perceber que o R1 fica "pendurado", ou seja, ele não contribui para o circuito, dessa forma a tensão em R é a tensão que fica em R2 pois eles ficam em paralelo! Igualzinho ao exercício anterior!
Para descobrirmos a tensão de R (Vth) então podemos multiplicar a corrente da fonte pelo valor de resistência de R2 já que o R1 tá fora da jogada:
Passo 3
Pronto, agora é só redesenhar o circuito de thévenin que conhecemos com os valores que encontramos:
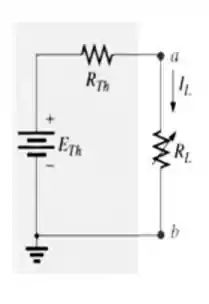
Passo 4
Com o circuito desenhado no passo anterior conseguimos calcular a corrente para diferentes valores de resistência fácil fácil pois vira um circuito série simples:
Para :
Para :
Para :
Resposta
a) ,
b) Para
Para
Para