Desenhe o circuito equivalente de Thévenin para o circuito externo ao resistor R nos dois circuitos mostrado na Figura 9.132
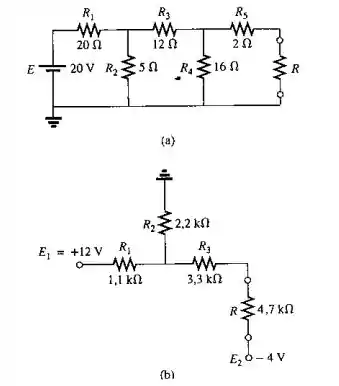
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
- Abra o circuito do resistor R e encontre o valor do resistor de Thévenin
- Curto circuite a fonte de tensão e abra o resistor R
Redesenhando como mostra na Figura 1
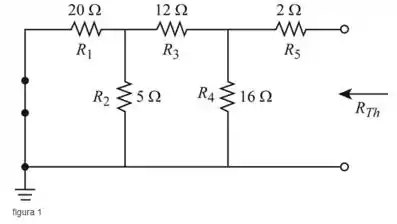
Encontraremos a resistência equivalente de Thévenin da rede
Redesenhe como mostrado na figura 2, e iremos encontrar a tensão de Thévenin
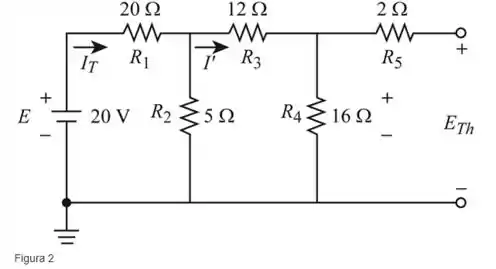
Passo 2
Iremos encontrar a resistência equivalente
Onde , nenhuma corrente flui através do resistor de e , portanto, pode ser desprezada
Aplicando a lei de Ohm, iremos encontrar a corrente total
Aplicando a regra de divisor de corrente
Aplicando a lei de Ohm
Desenhando o circuito equivalente de Thévenin (Figura 3)
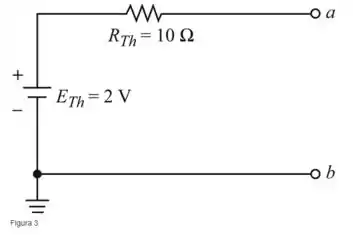
Passo 3
Redesenhe como mostrado a seguir (Figura 4)
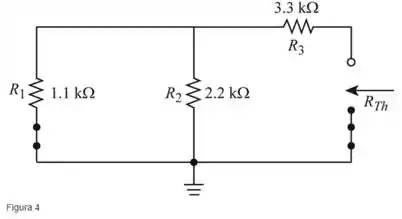
Encontrando a resistência equivalente de Thévenin
Aplicando o teorema da superposição iremos encontrar
Faça um curto circuito , e redesenhe como mostrado na figura a seguir (Figura 5).
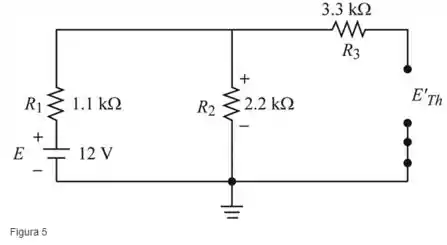
Passo 2
Aplicando a regra do divisor de tensão
Faça um curto circuito , e redesenhe como mostra a figura a seguir (Figura 6)
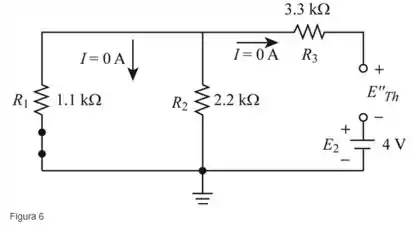
Onde o valor de é igual a tensão através da qual é igual a
Analisando a figura 5 e a figura 6. Ambas as tensões fluem na mesma direção
Desenhe o circuito equivalente, como mostra a figura 7.
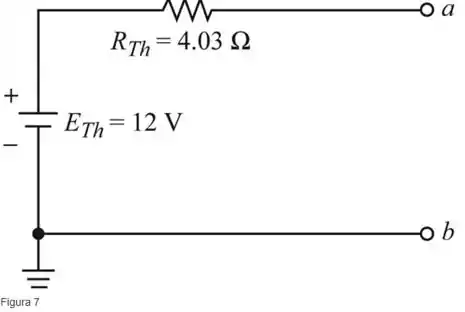
Resposta
- Figura 3
- Figura 7