- Desenhe o circuito equivalente de Thévenin para a parte do circuito externo ao resistor R nos circuitos mostrados na Figura 9.131.
- Faça a conversão para o circuito equivalente de Thévenin e compare os valores obtido de com os encontrados no Problema 7.
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
- Curto circuite as fontes de tensão de 15 V e 10 V e mantenha os terminais a e b abertos para encontrar o valor do resistor de Norton
-
- Abra a fonte de corrente do circuito e mantenha os terminais a e b abertos para encontrar o valor da resistência de Norton
- Usando a fórmuça e convertendo o circuito de Norton para Thévenin (I)
Redesenhe, como mostra na figura a seguir (Figura 4)
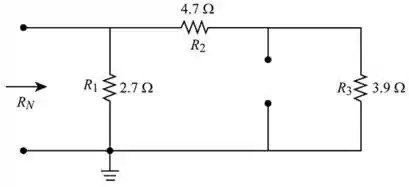
Passo 5
Iremos encontrar a resistência equivalente de Norton da rede
Redesenhe, como mostra na figura a seguir (Figura 5).
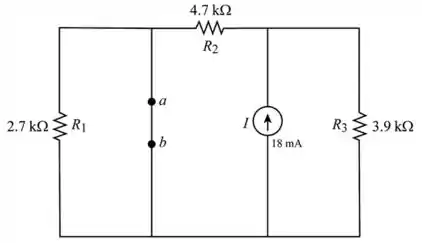
Passo 6
Aplicando a regra de divisão de corrente e encontrando o valor líquido da corrente que flui através dos terminais ab no circuito. Esta corrente dá o valor da corrente de Norton. Portanto, nenhuma corrente flui atráves de
Portanto, o valor da corrente de Norton é de
Desenhe o circuito equivalente de Thevenin como mostra na figura a seguir (Figura 6)
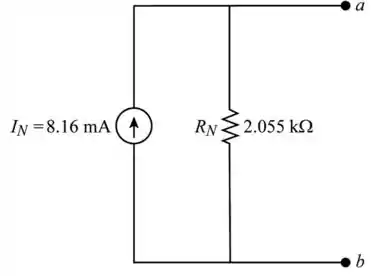
Passo 6
O valor de é igual a .
Desenhe o circuito equivalente de Thevenin como mostra na figura a seguir (Figura 7)
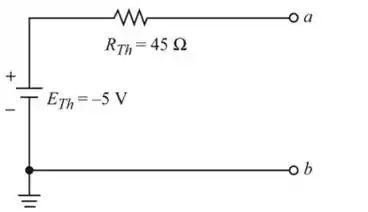
Assim, o circuito equivalente de Thévenin é desenhado e o valor é o mesmo quando comparado ao converter do equivalente de Norton.
Passo 7
- Usando a formula e convertendo o circuito equivalente de Norton para o Thévenin
Redesenhando , como mostrado a seguir (Figura 1)
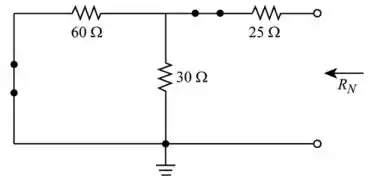
Passo 2
Vamos encontrar a resistência equivalente de Norton da rede
Redesenhando como mostra a figura a seguir (Figura 2), vamos encontrar a tensão de Thévenin
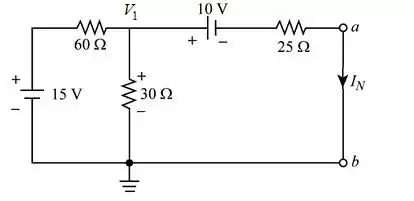
Passo 3
Aplicando a análise nodal no
Determinando o valor da corrente de Norton
Desenhando o circuito equivalente de Norton, como mostra a figura a seguir, (Figura 3)
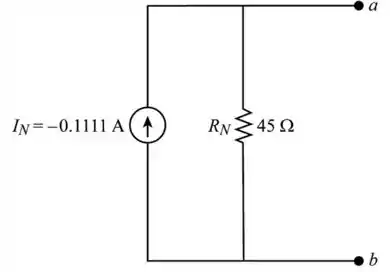
Passo 4
O valor de é igual a .
Desenhe o circuito equivalente de Thevenin como mostra na figura a seguir (Figura 8)
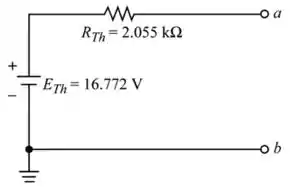
Assim, o circuito equivalente de Thévenin é desenhado e o valor é o mesmo quando comparado ao converter do equivalente de Norton.
Resposta
- Figura 6 e Figura 3.
- Figura 7 e Figura 8.