Desenhe o circuito equivalente de Thévenin para as partes dos circuitos da Figura 9.131 externas aos pontos a e b
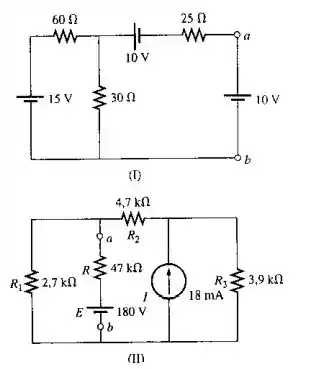
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
- Curto circuite as fontes de tensão de 15 V e 10 V e mantenha os terminais a e b abertos para encontrar o valor do resistor de Thévenin
- Abra a fonte de corrente do circuito e mantenha os terminais a e b abertos para encontrar o valor da resistência de Thévenin
Redesenhando , como mostrado a seguir (Figura 1)
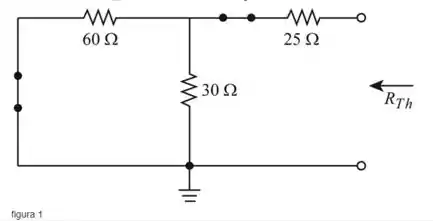
Passo 2
Vamos encontrar a resistência equivalente de Thévenin da rede
Redesenhando como mostra a figura a seguir (Figura 2), vamos encontrar a tensão de Thévenin
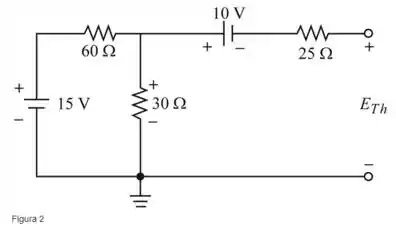
Passo 3
Onde, a queda de tensão no resistor de é zero, pois nenhuma corrente flui através do resistor.
A diferença entre a tensão através do resistor de é 10 V .
Aplicando a regra do divisor de tensão e encontraremos
Desenhando o circuito equivalente de Thévenin, como mostra a figura a seguir, (Figura 3)
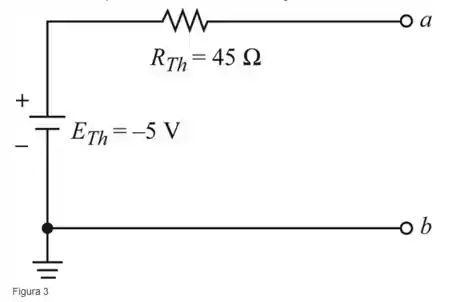
Passo 4
Redesenhe, como mostra na figura a seguir (Figura 4)
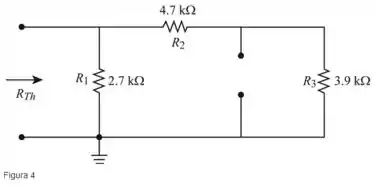
Passo 2
Iremos encontrar a resistência equivalente de Thévenin da rede
Redesenhe, como mostra na figura a seguir (Figura 5).
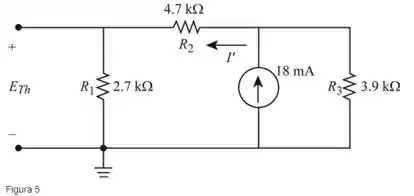
Passo 3
Vamos converter os resistores em série em um único elemento
Aplicando a regra de divisão de corrente e encontrando o valor líquido da corrente que flui no circuito
Aplicando a Lei de Ohm e encontrando o valor de
Desenhe o circuito equivalente de Thevenin como mostra na figura a seguir (Figura 6)
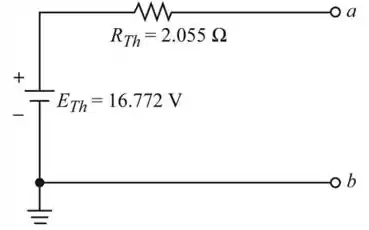
Resposta
- Figura 3
- Figura 7