Uma destas expressões é um campo eletrostático impossível. Qual delas?
(a);
(b) .
Aqui, é uma constante com as unidades adequadas. Para o campo possível, encontre o potencial usando a origem como seu ponto de referência. Verifique suas respostas calculando . [Dica: você deve escolher um caminho específico para a integração. Não importa qual é esse caminho, já que a resposta é independente do caminho escolhido, mas simplesmente não se pode integrar sem ter um caminho particular em mente.]
Passo 1
Falaaa, tudo belezaa?? Para descobrirmos qual dos campos elétricos podem ser eletroestáticos devemos calcular o rotacional deles. Caso seja diferente de zero, então, não pode ser um campo eletroestático.
Para a segunda parte da questão, sabemos que o potencial elétrico é dado por:
Vamos precisar fazer algumas interpretações para montar a integral, mas nada demais. Bora lá!!!
Passo 2
Colocando o rotacional dos campos elétricos.
Então, o campo elétrico 1 não pode ser um campo eletroestático!!
Calculando do segundo campo elétrico.
Então, o campo elétrico 2 é um possível campo eletrostático.
Passo 3
Agora vamos calcular o potencial elétrico para um caminho aleatório.
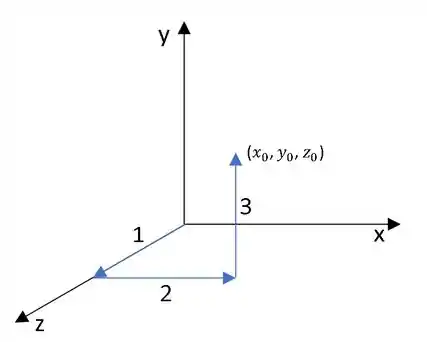
Perceba que no caminho 1, e até o final, não variam, . Então:
Como
Para o caminho 2, e agora o varia até . Porém, . E .
Integrando para achar o potencial.
Agora só precisamos encontra o do caminho 3, quem varia é .Onde, e .
Integrando.
Sendo assim, o potencial elétrico é dado como:
Ou também pode ser escrito como: