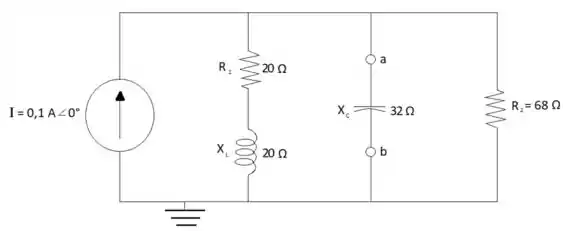
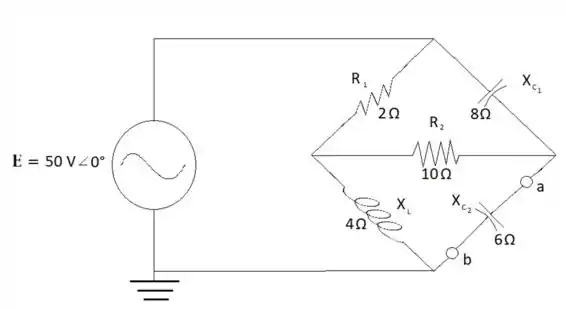
Determine o circuito equivalente de Norton para o circuito externo aos elementos entre a e b para os circuitos vistos na Figura 18.121
Passo 1
Para encontrar o equivalente de Norton do primeiro circuito se retira R2 e a fonte de corrente para poder calcular a impedância equivalente:
Z1 = 20 + j20 = 28,284 Ω45°
Z2 = 68 Ω
ZN = Z1Z2 = 21,31 Ω32,2°
Para se calcular a corrente que passa pelo circuito de Norton se substitui o R2 por um curto-circuito e nota-se que a corrente que se une e se separa das impedâncias é a mesma que a da fonte de corrente, logo:
IN = 0,1 A0°
Passo 2
Para calcular o equivalente de Norton no segundo circuito é necessário retirar o capacitor e fazer um curto-circuito na fonte de tensão, dessa forma é possível calcular a impedância total. Entretanto este novo circuito apresenta no seu interior um circuito o que complica o cálculo da impedância, por isso é recomendável transformar esse circuito para o formato Y que facilita muito o cálculo, no final se terá a seguinte impedância:
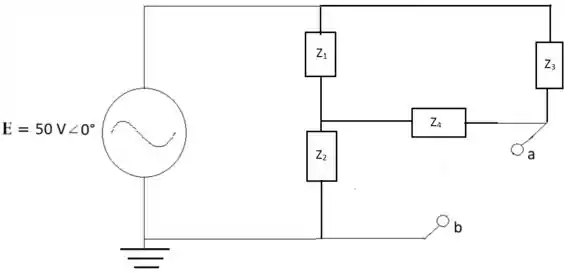
ZN = 3,98 Ω - j5,53 Ω
Passo 3
Para encontrar o valor de IN se substitui o capacitor de 6 Ω por um curto-circuito e dessa forma identifica-se por onde está passando a corrente. Com ajuda de um novo desenho do circuito identificamos o local e através de cálculos de divisor de corrente e tensão conseguimos encontrar o valor da corrente:
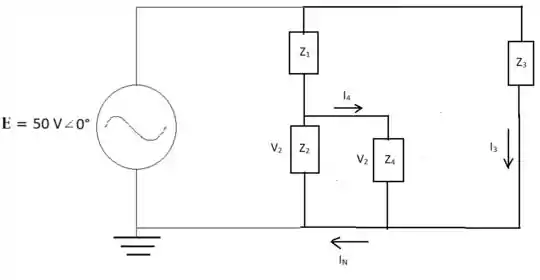
I3 = E/Z3 =6,250 A 90°
Z’ = Z2Z4 =3,714 Ω 68,2°
V2 = Z’E/(Z’ + Z1) = 38,471 V 22,612°
I4 = V2/Z4 = 3,847 A 22,612°
IN = I3 – I4 = 8,51 A 65,32°
Resposta
- ZN = 21,31 Ω32,2°
- ZN = 6,81 Ω-54,23°
IN = 0,1 A0°
IN = 8,51 A 65,32°