Determine o circuito equivalente de Norton para o circuito externo à reatância indutiva de , visto na Figura 18.116.
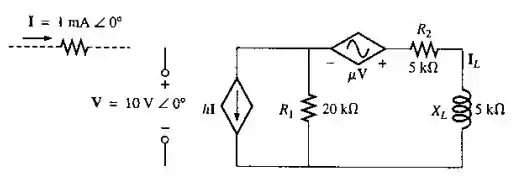
(Os valores das constantes e foram fornecidas em questões anteriores)
Passo 1
Falaaa, galera! Prontos para mais um exercício de circuitos?
Primeiro, vamos listar as impedâncias do circuito. Podemos ignorar o indutor pois estamos interessados no circuito externo ao mesmo.
Beleza, estamos prontos para descobrirmos os valores de corrente e impedância equivalentes de Norton para este circuito.
Passo 2
Vamos começar pela impedância. O primeiro passo é substituir o indutor por um circuito aberto e desligar as fontes. Assim, obtemos um curto circuito no lugar de e um circuito aberto no lugar de . Com isso, as impedâncias e ficam em série, de modo que:
Podemos então continuar para descobrir a corrente de Norton. Para isso, vamos substituir o indutor por um curto circuito.
Vamos utilizar o teorema da superposição. Desligando somente a fonte de tensão, vemos que a corrente da fonte irá se dividir entre as impedâncias. Como queremos a corrente que passa pela impedância , devemos calcular o seguinte divisor de corrente:
Agora, iremos desligar apenas a fonte de corrente. Aplicando a lei de Ohm, podemos determinar a corrente do circuito:
Como as correntes foram calculadas para sentidos opostos, teremos que: