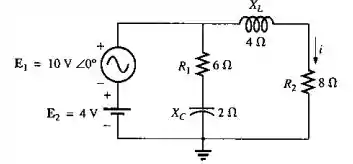
a. Determine o circuito equivalente de Thévenin para a parte do circuito externa ao resistor da Figura 18.111.
b. Usando os resultados do item (a), determine a corrente no mesmo circuito.
Passo 1
Fala, galera! Bora resolver mais uma questão de circuitos?
Vamos começar pela letra A. Primeiramente, vamos listar as impedâncias do circuito. Note que não precisamos incluir pois estamos interessados na parte externa à ele.
Para determinar a impedância , devemos desligar as fontes do circuito e analisar a impedância resultante.
Logo, desligando as fontes e , obtemos um curto circuito no lugar e podemos descartar (pois temos o paralelo com uma impedância nula) . Portanto:
Para determinar a tensão , vamos fazer uma análise simples. Note que a impedância está em paralelo com as fontes e Logo, a tensão em é e a tensão em é nula. Portanto:
Passo 2
Vamos então para o item B. Como e , temos um circuito com quatro elementos em série. Uma fonte AC de , uma fonte DC de , um indutor de e um resistor de .
Logo, a corrente no resistor será dada por:
Resposta
a.
b.