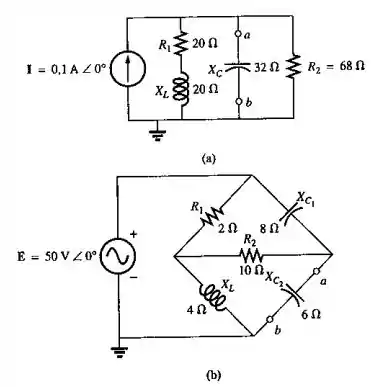
Determine o circuito equivalente de Thévenin para as partes dos circuitos vistos na Figura 18.121 externas aos elementos entre os pontos a e b.
Passo 1
Fala, pessoal! Mais uma questão de circuitos vindo por aí!
Começando pela letra A, vamos listar as impedâncias do circuito:
Como estamos interessados na parte externa ao terminal ab, podemos ignorar a impedância . Para determinar a impedância , devemos desligar as fontes e analisar a impedância resultante. Lembre-se que as fontes de corrente viram um circuito aberto e as fontes de tensão um circuito fechado, ok?
Note que desligando a fonte , e ficam em paralelo. Logo, teremos que:
Pela lei de Ohm, a tensão é o produto da impedância pela corrente fornecida pela fonte . Logo, temos que:
Passo 2
Vamos então seguir para a letra B. As impedâncias do circuito são:
A análise é similar, beleza? Vamos ignorar a impedância pois ela é interna ao terminal ab. Desligando a fonte , teremos as seguintes associações de impedância:
Observe que tensão é igual a soma das tensões sobre as impedância e . Note que a tensão se divide entre e a associação das demais impedâncias. Logo, a tensão em pode ser calculada utilizando o seguinte divisor de tensão:
Note que a tensão em se divide entre e .
Logo, a tensão em pode ser calculada utilizando o seguinte divisor de tensão:
Portanto:
Resposta
a.
b.