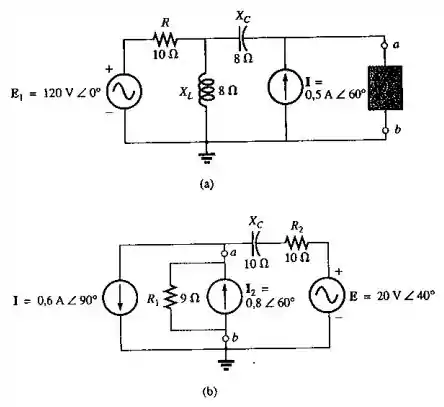
Determine o circuito equivalente de Thévenin para as partes dos circuitos vistos na Figura 18.122 externas aos elementos entre os pontos a e b.
Passo 1
E aí, pessoal! De boa? Prontos para mais uma questão de circuitos?
Vamos começar pela letra A. Dá uma olhada nas impedâncias desse circuito:
Para determinar a impedância , devemos desligar as fontes do circuito e analisar a impedância resultante. Lembre-se que as fontes de corrente viram um circuito aberto e as fontes de tensão um circuito fechado, ok?
Note que desligando as fontes e , e ficam em paralelo e a associação deles fica em série com . Teremos que:
Para determinar a tensão , vamos aplicar o teorema da superposição. Primeiro, vamos desligar a fonte . Note que a tensão será igual a tensão sobre a impedância . Logo, basta calcularmos o divisor de tensão:
Em nossa segunda análise, vamos desligar a fonte . Note que a tensão será igual a soma das tensões sobre as impedâncias e . Temos que:
Somando os resultados das duas análises, obtemos:
Passo 2
Vamos em frente que ainda temos a letra B!
Note que não estamos interessados nos elementos interiores ao terminal ab. Logo, teremos apenas uma impedância relevante nesse circuito:
Aplicando a LKT na malha da direita, obtemos:
Observe que invertemos o sinal da tensão pois estamos assumindo que a fonte fornece uma corrente no sentido da queda de tensão da impedância.
Resposta
a.
b.