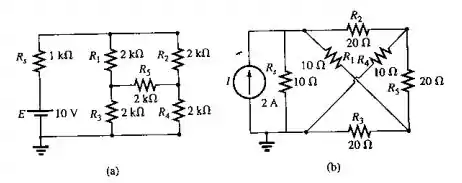
Determine a corrente na resistência interna da fonte para cada um dos circuitos mostrados na Figura 8.121 usando o método das malhas ou o método dos nós. Explique os motivos da sua escolha.
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
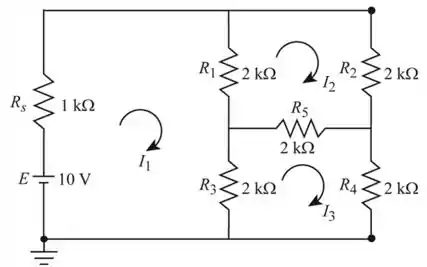
- Vamos redesenhar a figura, para determinar a corrente. A rede de ponte modificada é mostrada a seguir
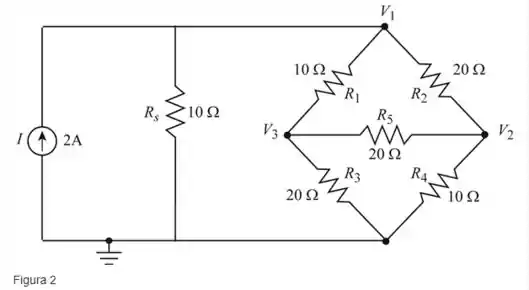
- Redesenhando a figura b para determinar a corrente. A rede de ponte modificada é mostrada a seguir
Passo 2
Vamos considerar o loop 1 na Figura anterior, para podermos encontrar a corrente usando a análise da malha.
Vamos considerar o loop 2 na Figura anterior, para podermos encontrar a corrente usando a análise da malha.
Vamos considerar o loop 3 na Figura anterior, para podermos encontrar a corrente usando a análise da malha.
Resolvendo a equação (1), equação (2), e equação (3), iremos encontrar os valores atuais correspondentes
Resolvendo esse sisteminha, temos que:
Portanto, os valores atuais são .
Passo 3
Vamos considerar a seguinte fórmula para encontrar a corrente através da resistência
Onde, a corrente através do valor da resistência é de .
Partindo da figura 1, não há necessidade de conversão de fonte usando o método de análise de malha. Sendo assim, optamos pelo método de análise de malha em detrimento do método de análise nodal.
Portanto, escolhemos o método de análise de malha sobre o método de análise nodal da Figura 1.
Passo 4
Passo 2
Vamos considerar o nó 1 da Figura 2, para encontrar a tensão usando a análise nodal.
Vamos considerar o nó 2 da Figura 2, para encontrar a tensão usando a análise nodal.
Vamos considerar o nó 3 da Figura 2, para encontrar a tensão usando a análise nodal.
Resolvendo a equação (1), equação (2), e equação (3), iremos encontrar os valores atuais correspondentes
Resolvendo esse sisteminha, temos que:
Portanto, os valores de tensão são .
Passo 3
Considerando a seguinte expressão
Assim, a corrente através do valor de resistência é
Partindo da figura 2, não há necessidade de conversão de fonte usando o método de análise de malha. Sendo assim, optamos pelo método de análise de malha em detrimento do método de análise nodal.
Portanto, escolhemos o método de análise de malha sobre o método de análise nodal da Figura 2.
Resposta
Vide as respostas ao final do passo 3 e do passo 6.