Determine a diferença de fase em milissegundos entre as seguintes formas de onda:
,
Passo 1
Saudações galerinha! tudo bem?
Antes de resolver essa questão, vamos só lembrar a expressão geral de uma senóide:
Onde:
é a amplitude senoidal
ω indica a frequência angular
Corresponde ao ângulo de fase
Pra te lembrar ainda mais vou te mostrar o gráfico da função senoidal coma expressão geral (1) acima.
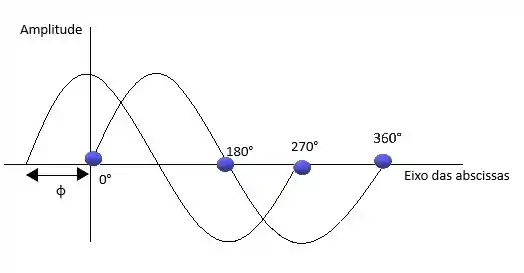
Neste caso os ângulos estão em graus
Bora começar então resolver nossa questão.
Em nossa questão temos duas funções diferentes uma seno e outra cosseno.
Para começar a analisar a relação de fase devo transformar a função em seno.
Para isso vou utilizar a transformação trigonométrica

Calma! Essa transformação trigonométrica é tranquila, borá lá aplicar
Prontinho, falei que era fácil!
Agora sim, vamos observar os ângulo de fase de , ou seja a tensão senoidal está atrasada em relação a corrente.
Vamos observar melhor essa relação no gráfico.
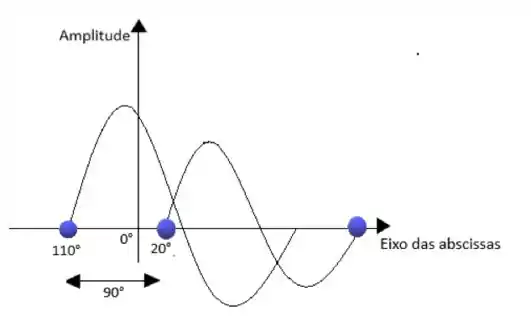
Dá para observar com esse gráfico que a diferença de fase entre suas funções é 90°, ou seja (110° -20°) = 90°
Temos agora que transformar esse ângulo de fase em milissegundos.
Próximo passo, siga minha astucia!
Passo 2
Como transformar 90 ° em milissegundos, paramos aqui lembra?
Então bora lá!
Ambas as formas de onda possuem a frequência angular será ω = 1800
Vou utilizar essa informação, para encontrar o período dessas ondas:
Lembrando da fórmula teremos:
Isolando o Período
Substituindo os valores
Vamos fazer uma regrinha de três e encerra nosso exercício.
360 ° corresponde a 3,49 ms que é o período das formas de onda, encontremos sua equivalência com 90°que é o ângulo de fase entre ambas.
Ângulo tempo
360°-------------3,49 x
90°---------------x
Aplicando meio por extremo, temos:
360 . X = 90 . 3,49 x
X =
Logo o = 87,25 ms
UFA! Acabou
Te vejo no próximo exercício.
Resposta
A diferença de fase é 87,25 ms