a) Determine as expressões matemáticas para e após a chave ser fechada no circuito visto na figura 12.79
b) Determine iL e vL após duas constantes de tempo da fase de armazenamento
c) Escreva as expressões matemáticas para a corrente e para a tensão se a chave for aberta no instante definido no item (b)
d) Esboce as formas de onda de e para os itens (a) e (c)
Passo 1
a) E aeeeeeee! Vamos lá, temos esse circuito aqui:
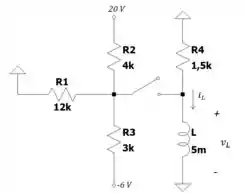
Vamos reorganizar isso aí pra ficar mais simples de visualizar? Hahahaha podemos desenhar assim olha:
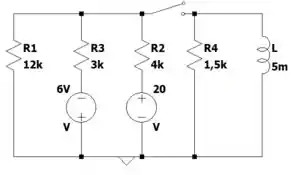
Como temos algumas fontes de tensão em série com resistores, podemos fazer a conversão para fontes de corrente, certo?
Para a fonte de , a fonte de corrente vai valer
Já para a fonte de , temos
Aí o circuito fica assim:
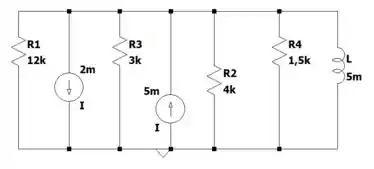
Opa que ainda dá pra continuar simplificando, vem comigo!
Passo 2
A corrente equivalente no circuito é
E a resistência equivalente vai ser
O que nos dá:
Olha que bonitinho que fica o circuito agora
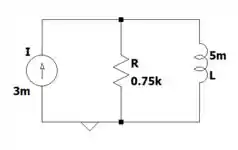
E aí fazendo conversão de fonte para uma fonte de tensão em série com o resistor, temos
E aí fica assim
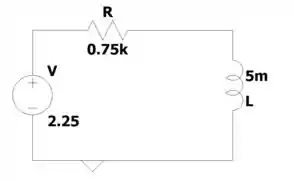
Agora simmm, podemos encontrar as expressões de e hahahahaha
Passo 3
A primeira coisa que precisamos é o valor de , ele vai ser dado por
Boaa, agora que temos o podemos encontrar as expressões que queremos. Para , vamos usar
Então, a expressão de é
Passo 4
Para , podemos usar
Substituindo os valores, temos a expressão de
Passo 5
b) Agora é só a gente usar as expressões do item anterior substituindo
Primeiro para :
Então:
Passo 6
Agora para :
Então
Passo 7
c) Agora é o seguinte: a chave vai ser aberta em
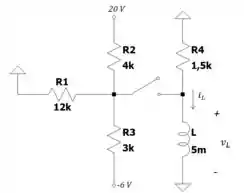
Quando isso acontecer, temos e , então nosso novo vai ser
Para encontrarmos as expressões de e de , precisamos do valor de e de em
Para , já calculamos no item anterior, vale
Para em , podemos fazer
Então, quando a chave é aberta vamos ter
Sacou?
Passo 8
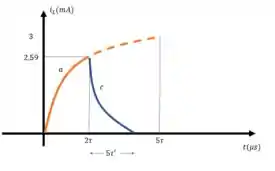
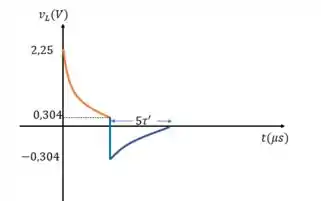
d) Por fim, vamos traçar os gráficos para as letras a e c:
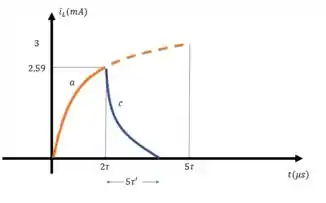
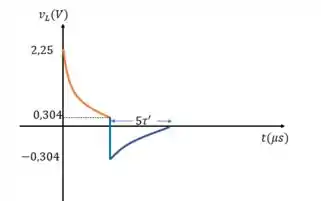
E acabaaamos, fechou?
Resposta
a)
b)
c)
d)