Determine, para a forma de onda pulsada vista na figura :
a) Se os pulsos são positivos ou negativos;
b) O nível da base;
c) A largura dos pulsos;
d) A amplitude dos pulsos;
e) A inclinação percentual dos pulsos;
Passo 1
Saudações galerinha, tudo bem?
Vamos começar a resolver mais um exercício, bora lá então!
(a) Inicialmente começaremos a observar o gráfico mostrado no livro que representa a figura , a primeira alternativa é apenas para classificar o pulso como positivo ou negativo.
No gráfico o pulso é positivo, pois a amplitude da mesma é maior que zero.
Tranquilo né, vamos para próxima alternativa!
Passo 2
(b) Em nossa segunda alternativa devemos identificar o nível de base. Para isso vamos observar o gráfico mais uma vez.
Lembrando que o nível de base nada mais é do que o valor pelo qual o pulso começa. Notamos em nosso gráfico que o nosso pulso começa em .
Logo o nível de base deste gráfico é .
Passo 3
(c) A largura do pulso é a distância que representa da amplitude do pulso, vamos observar a imagem exemplo e entender melhor:
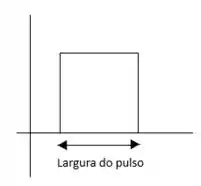
Não podemos esquecer que para encontrar a largura do pulso, devemos focar no eixo horizontal do gráfico, beleza!
Focando nossos olhares para o gráfico observamos que a largura do pulso será .
Quase acabamos, vamos para próxima alternativa!
Passo 4
(d) Só lembrando que a amplitude de um pulso é o valor pico a pico menos o valor do nível de base, vamos focar no gráfico da questão podemos notar que o maior valor exibido no eixo vertical, representa o valor pico a pico
Logo:
A amplitude será (valor máximo do eixo vertical – valor do nível de base)
A amplitude
Passo 5
Ufa, essa é a última!
Antes de começamos vamos relembra como podemos encontrar a inclinação percentual, a fórmula está descrita abaixo:
Onde:
V é o valor médio =
Voltando a questão podemos identificar os valores em nosso gráfico
Encontrando o valor médio:
Aplicando na formula da inclinação teremos:
Resposta
(a) Pulso positivo
(b) nível de base
(c) Largura do pulso
(d)Amplitude
(e) Inclinação