a. Determine a impedância da carga que, ao substituir a impedância no circuito visto na Figura 18.112, garante a máxima potência na carga.
b. Usando os resultados do item (a), determine o valor da potência máxima na carga.
Passo 1
Fala, pessoal! Prontos para mais uma questão de circuitos?
Primeiro, vamos chamar a impedância da carga que substitui de . Lembre-se que a máxima transferência de potência para carga ocorre quando . Logo, devemos obter o circuito equivalente de Thévenin para o circuito externo à carga de interesse.
Vamos listar as impedâncias desse circuito, externas à .
Passo 2
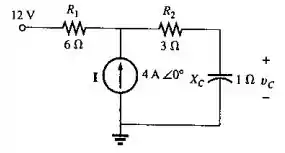
Vamos começar por . Desligando as fontes e de , obtemos um circuito aberto e um curto circuito em seus lugares, respectivamente. Com isso, e ficam em série, de modo que:
Assim, e
Em seguida, vamos fazer uma análise DC e uma análise AC do circuito para determinar . Em ambos os casos, devemos substituir a carga por um circuito aberto e analisar seus terminais.
Passo 3
Desligando somente a fonte de corrente, vemos que a tensão DC de Thévenin é igual a de entrada, de 12V.
Desligando somente a fonte de 12V, podemos notar que nenhuma corrente passa por , graças ao circuito aberto no lugar da carga. Logo, a tensão AC de Thévenin é dada pela lei de Ohm:
Portanto,
Logo, a potência máxima fornecida à carga é de: