Determine a potência média fornecida a no circuito mostrado na Figura .
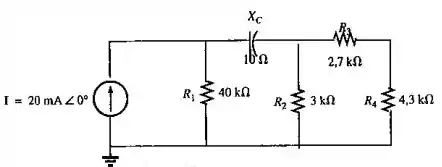
Passo 1
Observe atentamente a figura do enunciado. Podemos arranja-la da seguinte forma:
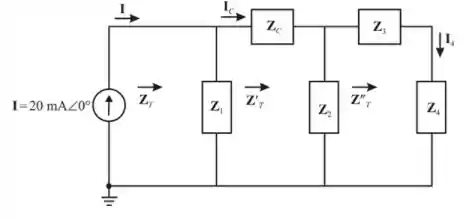
Agora que demos nomes aos bois, vamos aos cálculos:
Passo 2
Agora vamos calcular . Temos que:
Passo 3
Logo:
Passo 4
Podemos calcular a corrente :
Portanto, a potência entregue ao resistor , vale: