Determine as quantidades desconhecidas no circuito mostrado na Figura 5.82 usando as informações fornecidas.
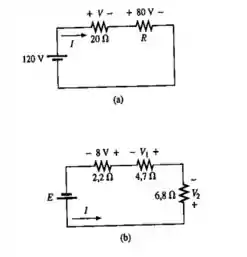
Passo 1
- Aplicaremos a lei das tensões de Kirchhoff ao circuito e iremos encontrar o valor de V.
- Vamos encontrar E
- Aplicando a lei de Ohm, iremos encontrar
- Considerando o resistor de iremos encontrar no circuito
Vamos usar a seguinte expressão e encontrar R
Portanto, o valor de é 40 V, e é de .
Passo 2
Passo 3
Vamos encontrar
Passo 4
Vamos encontrar
Passo 5
Aplicando a lei de Ohm e encontrando a corrente
Portanto, o valor de .
Passo 6
Aplicando a lei de Ohm, iremos encontrar
Passo 7
Agora iremos encontrar R
Aplicando a lei de Ohm, iremos encontrar
Portanto, as tensões são , respectivamente e a resistência desconhecida .
Passo 8
Vamos encontrar o
Passo 2
Todas as resistências estão conectadas em série e a resistência total é . Portanto, iremos encontrar .
Usando a lei de Ohm, iremos encontrar E
Portanto, a corrente , e a tensão de alimentação .
Resposta
- Portanto, o valor de é 40 V, e é de .
- Portanto, o valor de .
- Portanto, as tensões são , respectivamente e a resistência desconhecida .
- Portanto, a corrente , e a tensão de alimentação .