Determine a tensão nos elementos vistos na Figura 15.115 usando a álgebra dos números complexos. Esboce as formas de onda de e no mesmo gráfico.
Passo 1
Oi tudo bem??
Vamos lá!!
- Considere o valor da corrente fluindo através da resistência
- Considerando o valor da corrente fluindo através da indutância
- Considerando o valor da corrente fluindo através da capacitância
Escreveremos a forma fasorial da tensão a partir da tensão no domínio do tempo.
Substituindo na equação (1)
Escreva a impedância de R na forma polar.
Escreva a fórmula da tensão fasorial para carga resistiva.
Substituindo na expressão (3)
Faça á fórmula para v no domínio do tempo de fasor corrente V.
Portanto, o valor da tensão na resistência é
Passo 2
Escreva a forma polar de de
Substituindo na expressão (5)
Consulte a Fig 15.114 (b) no livro.
Escreva o valor da indutância
Escreva a fórmula para reatância indutiva .
Substitua na equação (6)
Escreva o valor polar da impedância da reatância indutiva.
Escreva a fórmula para V partindo da reatância indutiva
Substituindo na expressão (7)
Escreva a equação da tensão partindo da tensão fasorial.
Portanto, o valor da tensão no indutor é de .
Passo 3
Substituindo na equação (5)
Consulte a Fig 15.114 (c) no livro .
Escreveremos o valor da capacitância.
Escreveremos a fórmula para a reatância capacitiva .
Substituindo na equação (8)
Escreveremos o valor polar da impedância da reatância capacitiva
Escreveremos á formula para V partindo da reatância capacitiva
Substituindo na equação (9)
Escreveremos a equação da tensão partindo da tensão fasorial.
Portanto, o valor da tensão no indutor é .
Passo 2
Desenharemos as tensões e formas de onda atuais dos valores calculados nos passos anteriores.
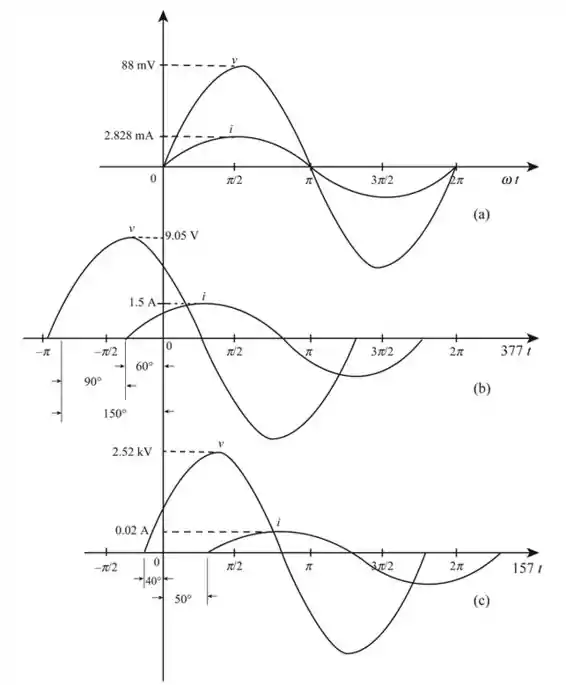
Consequentemente, as tensões e as formas de onda da corrente são desenhadas.
Resposta
Ei, a resposta está no passo a passo :)