Determine os valores de para o divisor de tensão mostrado na Figura 5.89 se a corrente da fonte for 16 mA.
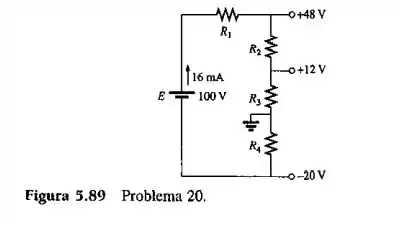
Passo 1
Vamos desenhar o diagrama de circuito modificado
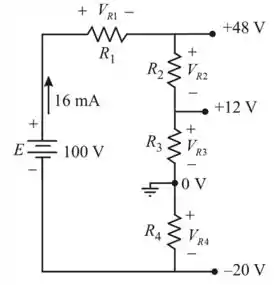
Passo 2
A tensão no resistor é
Determine o valor do resistor
Portanto, o valore do resistor .
Passo 3
A tensão no resistor é
Determine o valor do resistor
Portanto, o valore do resistor .
Passo 4
A tensão no resistor é
Determine o valor do resistor
Portanto, o valore do resistor .
Passo 5
Aplicando a lei de tensão de Kirchhoff na figura do passo 1
Passo 6
Determinando o valor do resistor
Portanto, o valor de .
Resposta
Portanto, o valore do resistor .
Portanto, o valore do resistor .
Portanto, o valore do resistor .
Portanto, o valor de .