Um dipolo elétrico ideal está localizado na origem e aponta na direção z, como na Figura 3.36. Uma carga elétrica é liberada do repouso em um ponto no plano xy. Mostre que ela balança para a frente e para trás em um arco semicircular, como se fosse um pêndulo sustentado na origem. [O crédito deste resultado encantador é de R. S. Jones, Am. J. Phys. 63, 1042 (1995).]
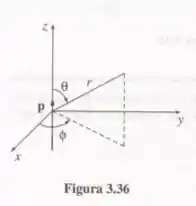
Passo 1
Olá pessoal, bora para mais uma!?
Podemos partir de
Substituindo o campo, temos que:
Agora considerando o pendulo: , onde temos que:
e
Mas como temos:
Assim:
E assim, temos:
Esta força total é tal que mantém o pêndulo em um arco circular, e é idêntica à força sobre no campo de um dipolo, com Evidentemente a carga q também irá executar movimento circular, como se estivesse em uma corda de comprimento fixo .
Assim finalizamos mais uma! Até a próxima!
Resposta
Desenvolvimento no passo 1.