Dois fios de comprimento infinito dispostos paralelamente ao eixo x têm densidades de carga uniforme e (figura 2.54).
(a) Encontre o potencial em qualquer ponto (x, y, z) usando a origem como referência.
(b) Mostre que as superfícies equipotenciais são cilindros circulares e encontre o eixo e o raio do cilindro que correspondem a um dado potencial
Passo 1
Faaala, galera! Bora pra mais uma. Inicialmente, para encontrar o potencial para o potencial em qualquer ponto, precisamos lembrar da expressão do campo elétrico:
Aplicando essa expressão na equação do potencial elétrico e considerando um ponto de referência (origem no nosso caso), teremos:
Resolvendo essa integral, teremos:
Com isso, substituído os valores de , teremos:
Para :
Para :
Logo, o potencial total será dador, por:
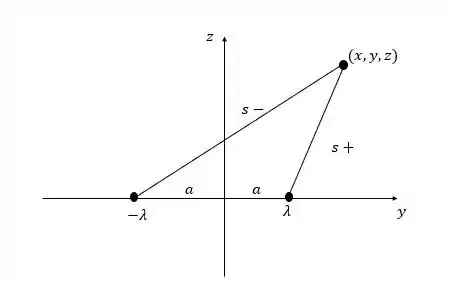
Como queremos para um ponto qualquer , teremos que encontrar expressões para as distâncias . Para encontrarmos essas expressões, podemos usar o esquema apresentado no inicio da página para chegarmos a:
E agora, substituindo essas expressões na equação que encontramos para o potencial total, teremos:
Passo 2
Agora que temos a expressão para o potencial em qualquer ponto, vamos igualar a equação do potencial a 0 (já que na superfície equipotencial não existe diferença de potencial):7
E agora aplicando o exponencial em ambos os lados e rearrumando, teremos:
Com essa expressão, podemos passar o denominador para o outro lado multiplicando o k, para ficarmos com:
Passando os termos encontrados na direita para a esquerda da equação, teremos:
E rearrumando agora a equação que obtivemos:
Dividindo os dois lados por :
Agora, podemos comparar essa equação com a equação de um círculo centrado em de raio , que tem a seguinte forma:
Ou expandindo o termo :
Comparando essa expressão com a equação (1) que obtivemos para as equipotenciais, podemos ver que elas são equivalentes, com:
Também podemos fazer a seguinte equivalência:
Isolando :
Agora substituindo o encontrado anteriormente nessa expressão, vamos ter:
Logo, o raio será:
Agora, para colocarmos e em termos de basta substituirmos a constante pela exponencial do início e com isso, teremos:
E:
Ou seja:
Que denotam um cilindro.
E aqui chegamos ao fim da questão, galera! Até a próxima 😊
Resposta
a)
b)