Encontre o campo elétrico a uma altura do centro de uma folha quadrada (lado a) que tem uma carga superficial de densidade uniforme . Verifique seu resultado para os casos limites
Passo 1
Faaala, galera! Bora pra mais uma. Primeiramente, vamos ter que o campo elétrico a uma altura de um segmento de reta (de comprimento 2L) será dado por:
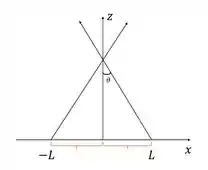
No nosso caso, como queremos para um dos lados da folha (de lado ), teremos que a distância de -L até L será igual a , portanto:
A distância de para a reta será dada por:
Portanto substituindo os valores na primeira expressão, teremos:
Para termos apenas a componente vertical, multiplicaremos a expressão acima pelo cosseno de , e teremos:
Logo:
Como queremos o campo para um ponto no centro de uma folha quadrada (que funciona como uma espira quadrada) de lado , teremos que multiplicar a expressão acima por 4, pois teremos quatro segmentos de reta nesse caso (4 lados da espira ou folha), logo, teremos:
Passo 2
Podemos ver pelo esquema abaixo, que a densidade linear de carga será dada por:
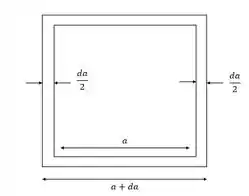
Passo 3
Agora substituindo a expressão pra lambda na expressão do campo elétrico teremos:
Rearrumando teremos:
Agora integraremos a expressão de 0 até a
Para resolver essa integral, usaremos a técnica da substituição de variável. Considerando:
Com isso:
Substituindo na integral, teremos:
Integrando, teremos:
Passo 4
Com a expressão obtida, agora, faremos os testes para os seguintes casos:
Primeiro, para o caso , teremos:
Para o caso , teremos:
Considerando e expandido em uma série de Taylor:
Para , , terá o seguinte valor:
E para :
Logo, . Aplicando os valores na série de Taylor e levando em conta que:
Teremos que:
Resposta
Para :
Para :